george visvikis έγραψε: ↑Τρί Μαρ 02, 2021 10:37 am
Ίσοι και εφαπτόμενοι.png

είναι το ύψος ισοσκελούς τριγώνου

με
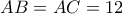
και

Επί της πλευράς

θεωρώ τα σημεία

ώστε

Ι) Να κατασκευάσετε κύκλο

που να διέρχεται από τα σημεία

και να εφάπτεται στις ευθείες

και να υπολογίσετε την ακτίνα του.
II) Να δείξετε ότι ο κύκλος που διέρχεται από τα σημεία

εφάπτεται στον

και είναι ίσος με αυτόν.

- Επαφή και ίσοι 1.png (22.47 KiB) Προβλήθηκε 545 φορές
α) Γράφω τυχαίο κύκλο δια των

( παράδειγμα με διάμετρο το
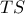
) και φέρνω το εφαπτόμενο τμήμα από το

εφαπτόμενο τμήμα

.
Γράφω, μετά , τον κύκλο

που τέμνει την ευθεία

σε δύο σημεία ,

εκτός και εντός του τριγώνου

και είναι η άλλη κορυφή των ζητούμενων κύκλων .
Απόδειξη :
Επειδή

οι κύκλοι :

εφάπτονται στην

στα σημεία

.
Οι κύκλοι αυτοί εφάπτονται , λόγω συμμετρίας και στην

ενώ το κέντρο του μεγάλου κύκλου , έστω

, θα ανήκει στη διχοτόμο της γωνίας

.
Υπολογισμός ακτίνας

- Επαφή και ίσοι 2.png (23.96 KiB) Προβλήθηκε 545 φορές
Προφανώς το τετράπλευρο

είναι ισοσκελές τραπέζιο οπότε και το

είναι ισοσκελές . Αβίαστα προκύπτουν:

και



και

Από το τύπο του Ήρωνα στο
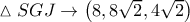
και τον τύπο

έχω:

Και πάμε τώρα στο ωραίο μέρος .
Επειδή

συνεπώς και το

είναι ισοσκελές άρα τα

ανήκουν στην ίδια ευθεία .

- ϊσοι και εφάπτοντα_τελικό.png (36.24 KiB) Προβλήθηκε 545 φορές
Επειδή τώρα το τρίγωνο

και το

μέσο του

θα είναι :

και άρα οι κύκλοι τους είναι ίσοι και ο δεύτερος περνά από το

Γιατί ,

Επίσης αν

το συμμετρικό του

ως προς το

έχω:

.
Συνεπώς

όμως

, δηλαδή η

είναι μεσοκάθετος στο

και άρα το

είναι το κέντρο του κύκλου

 είναι το ύψος ισοσκελούς τριγώνου
είναι το ύψος ισοσκελούς τριγώνου  με
με 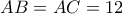 και
και  Επί της πλευράς
Επί της πλευράς θεωρώ τα σημεία
θεωρώ τα σημεία  ώστε
ώστε 
 που να διέρχεται από τα σημεία
που να διέρχεται από τα σημεία  και να εφάπτεται στις ευθείες
και να εφάπτεται στις ευθείες και να υπολογίσετε την ακτίνα του.
και να υπολογίσετε την ακτίνα του. εφάπτεται στον
εφάπτεται στον  και είναι ίσος με αυτόν.
και είναι ίσος με αυτόν.
 . Επειδή :
. Επειδή :  ,
, . Έτσι κατασκευάζουμε τον κόκκινο κύκλο , για του οποίου η ακτίνα είναι :
. Έτσι κατασκευάζουμε τον κόκκινο κύκλο , για του οποίου η ακτίνα είναι :  .
. , οπότε :
, οπότε :  και τελικά :
και τελικά :  .
. και με Ήρωνα , ότι :
και με Ήρωνα , ότι :  , οπότε :
, οπότε :  .
.

 και στο σημείο
και στο σημείο  με ακτινα
με ακτινα  προσδιορίζουμε το κέντρο
προσδιορίζουμε το κέντρο 


 είναι συνευθειακά
είναι συνευθειακά  Αρα το ορθογώνια τρίγωνα
Αρα το ορθογώνια τρίγωνα  είναι ίσα και
είναι ίσα και
 είναι συνευθειακά .Τέλος
είναι συνευθειακά .Τέλος ( παράδειγμα με διάμετρο το
( παράδειγμα με διάμετρο το 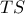 ) και φέρνω το εφαπτόμενο τμήμα από το
) και φέρνω το εφαπτόμενο τμήμα από το  εφαπτόμενο τμήμα
εφαπτόμενο τμήμα  .
. που τέμνει την ευθεία
που τέμνει την ευθεία  σε δύο σημεία ,
σε δύο σημεία ,  εκτός και εντός του τριγώνου
εκτός και εντός του τριγώνου 
 οι κύκλοι :
οι κύκλοι :  εφάπτονται στην
εφάπτονται στην  .
. ενώ το κέντρο του μεγάλου κύκλου , έστω
ενώ το κέντρο του μεγάλου κύκλου , έστω  .
. είναι ισοσκελές τραπέζιο οπότε και το
είναι ισοσκελές τραπέζιο οπότε και το  είναι ισοσκελές . Αβίαστα προκύπτουν:
είναι ισοσκελές . Αβίαστα προκύπτουν: και
και 

 και
και 
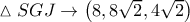 και τον τύπο
και τον τύπο  έχω:
έχω: 

 είναι ισοσκελές άρα τα
είναι ισοσκελές άρα τα  ανήκουν στην ίδια ευθεία .
ανήκουν στην ίδια ευθεία .
 και το
και το  μέσο του
μέσο του  θα είναι :
θα είναι : και άρα οι κύκλοι τους είναι ίσοι και ο δεύτερος περνά από το
και άρα οι κύκλοι τους είναι ίσοι και ο δεύτερος περνά από το 
 το συμμετρικό του
το συμμετρικό του  .
. όμως
όμως  , δηλαδή η
, δηλαδή η  είναι μεσοκάθετος στο
είναι μεσοκάθετος στο 