KARKAR έγραψε: ↑Σάβ Φεβ 06, 2021 1:51 pm
Περιακτίνα.pngΗ πλευρά

του τριγώνου

είναι σταθερή , ενώ οι

έχουν σταθερό άθροισμα

.
Ο περίκυκλος του τριγώνου έχει ακτίνα

, ( χρησιμοποιήσαμε τον όρο
περιακτίνα )
Α) ι) Αν

, λύστε ως προς

, την εξίσωση :

ιι) Υπολογίστε το ελάχιστο μήκος της

.
Β) Αν

, υπολογίστε το ελάχιστο μήκος της

. Σχολιάστε ...
Περιακτίνα
Στην περίπτωση του σταθερού

και μόνο για τον υπολογισμό του

.
Α1) Θεωρώ σύστημα αξόνων με αρχή το μέσο

του

και οριζόντιο άξονα την ευθεία

.
Με κέντρο το

γράφω κύκλο με ακτίνα

που τέμνει τον κατακόρυφο άξονα στο

. Στον ίσο κύκλο

θα ανήκει το

.
Επειδή όμως το άθροισμα των αποστάσεών του από τα

είναι

θα ανήκει και στην έλλειψη μ εξίσωση

.

- περιακτίνα_A_1.png (36.54 KiB) Προβλήθηκε 330 φορές
Από το σύστημα :

προκύπτει τελικά :

ή συμμετρικά .
Α2) και Β

- περιακτίνα_A_2 B.png (20.67 KiB) Προβλήθηκε 330 φορές
Το κέντρο

του κύκλου θα ανήκει στην σταθερή μεσοκάθετο ,
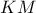
του

η οποία τέμνει τον κύκλο στο βόρειο πόλο , έστω

.
Για να πετύχω την πιο μικρή τιμή του

αρκεί το

να στηθεί στο

.
Τότε

. Έτσι
Αν

, έχω:

, ενώ αν

έχω:

.
 του τριγώνου
του τριγώνου  είναι σταθερή , ενώ οι
είναι σταθερή , ενώ οι  έχουν σταθερό άθροισμα
έχουν σταθερό άθροισμα  .
. , ( χρησιμοποιήσαμε τον όρο περιακτίνα )
, ( χρησιμοποιήσαμε τον όρο περιακτίνα ) , λύστε ως προς
, λύστε ως προς  , την εξίσωση :
, την εξίσωση : 
 .
. , υπολογίστε το ελάχιστο μήκος της
, υπολογίστε το ελάχιστο μήκος της  . Σχολιάστε ...
. Σχολιάστε ...

 ή
ή  και το τρίγωνο που προκύπτει είναι ορθογώνιο.
και το τρίγωνο που προκύπτει είναι ορθογώνιο.  ενώ Β) για
ενώ Β) για 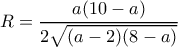
 και είναι
και είναι 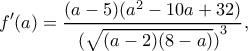 απ' όπου προκύπτει ότι
απ' όπου προκύπτει ότι παρουσιάζει ελάχιστο. Έτσι έχουμε για την πρώτη περίπτωση
παρουσιάζει ελάχιστο. Έτσι έχουμε για την πρώτη περίπτωση  και για τη δεύτερη
και για τη δεύτερη 
 και μόνο για τον υπολογισμό του
και μόνο για τον υπολογισμό του  του
του  και οριζόντιο άξονα την ευθεία
και οριζόντιο άξονα την ευθεία  γράφω κύκλο με ακτίνα
γράφω κύκλο με ακτίνα  που τέμνει τον κατακόρυφο άξονα στο
που τέμνει τον κατακόρυφο άξονα στο  . Στον ίσο κύκλο
. Στον ίσο κύκλο  θα ανήκει το
θα ανήκει το  .
.  είναι
είναι  .
.

 ή συμμετρικά .
ή συμμετρικά .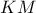 του
του  .
. . Έτσι
. Έτσι  , έχω:
, έχω:  , ενώ αν
, ενώ αν  έχω:
έχω:  .
.