 . Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.Ανισότητα σε τραπέζιο
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Ανισότητα σε τραπέζιο
Οι διαγώνιοι ενός τραπεζίου τέμνονται υπό γωνία  . Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
 . Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.Λέξεις Κλειδιά:
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Ισχύει και όταν οι διαγώνιοι του τραπεζίου τέμνονται σε γωνία μικρότερη τωνAl.Koutsouridis έγραψε: ↑Παρ Δεκ 18, 2020 11:08 pmΟι διαγώνιοι ενός τραπεζίου τέμνονται υπό γωνία. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
 : τα 'κρίσιμα' τρίγωνα είναι τα
: τα 'κρίσιμα' τρίγωνα είναι τα  και
και  (όπου
(όπου  ,
,  οι παράλληλες πλευρές και
οι παράλληλες πλευρές και  το σημείο τομής των διαγωνίων), καθώς, λόγω της
το σημείο τομής των διαγωνίων), καθώς, λόγω της  ... οφείλουν να ισχύουν είτε οι
... οφείλουν να ισχύουν είτε οι  είτε οι
είτε οι  , οπότε αντίστοιχα είτε
, οπότε αντίστοιχα είτε  ,
,  είτε
είτε  ,
,  , δηλαδή είτε
, δηλαδή είτε  είτε
είτε  -- το άθροισμα των βάσεων οφείλει να είναι μικρότερο ή ίσο είτε της μιας διαγωνίου είτε της άλλης, με ανάλογο (και πιο άμεσο) όμως συλλογισμό στα αμβλυγώνια τρίγωνα
-- το άθροισμα των βάσεων οφείλει να είναι μικρότερο ή ίσο είτε της μιας διαγωνίου είτε της άλλης, με ανάλογο (και πιο άμεσο) όμως συλλογισμό στα αμβλυγώνια τρίγωνα 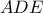 ,
,  ... η κάθε διαγώνιος οφείλει να είναι μικρότερη του αθροίσματος των μη παραλλήλων πλευρών.
... η κάθε διαγώνιος οφείλει να είναι μικρότερη του αθροίσματος των μη παραλλήλων πλευρών.Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ανισότητα σε τραπέζιο
Καλησπέρα σε όλους!
Νομίζω ότι πρώτα πρέπει να ξεκαθαρίσουμε (επειδή η εκφώνηση δεν είναι σαφής) ότι η γωνία των είναι εκείνη που βαίνει στις βάσεις και όχι στις μη παράλληλες πλευρές, όπου έχουμε το ακριβώς αντίθετο αποτέλεσμα. Υποθέτω επίσης ότι μιλάμε για το άθροισμα των βάσεων.
είναι εκείνη που βαίνει στις βάσεις και όχι στις μη παράλληλες πλευρές, όπου έχουμε το ακριβώς αντίθετο αποτέλεσμα. Υποθέτω επίσης ότι μιλάμε για το άθροισμα των βάσεων.
Νομίζω ότι πρώτα πρέπει να ξεκαθαρίσουμε (επειδή η εκφώνηση δεν είναι σαφής) ότι η γωνία των
 είναι εκείνη που βαίνει στις βάσεις και όχι στις μη παράλληλες πλευρές, όπου έχουμε το ακριβώς αντίθετο αποτέλεσμα. Υποθέτω επίσης ότι μιλάμε για το άθροισμα των βάσεων.
είναι εκείνη που βαίνει στις βάσεις και όχι στις μη παράλληλες πλευρές, όπου έχουμε το ακριβώς αντίθετο αποτέλεσμα. Υποθέτω επίσης ότι μιλάμε για το άθροισμα των βάσεων.- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ανισότητα σε τραπέζιο
Καλησπέρα!
Εφόσον δεν διευκρινίζεται στην εκφώνηση για για ποιά από τις δυο γωνίες είναι , θα πρέπει να εξεταστούν και οι δυο. Αν το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο ή ίσο της μεγαλύτερης βάσης, τότε θα είναι και της μικρότερης. Οπότε, όχι, δε μιλάμε για το άθροισμα των βάσεων.
, θα πρέπει να εξεταστούν και οι δυο. Αν το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο ή ίσο της μεγαλύτερης βάσης, τότε θα είναι και της μικρότερης. Οπότε, όχι, δε μιλάμε για το άθροισμα των βάσεων.
Εφόσον δεν διευκρινίζεται στην εκφώνηση για για ποιά από τις δυο γωνίες είναι
 , θα πρέπει να εξεταστούν και οι δυο. Αν το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο ή ίσο της μεγαλύτερης βάσης, τότε θα είναι και της μικρότερης. Οπότε, όχι, δε μιλάμε για το άθροισμα των βάσεων.
, θα πρέπει να εξεταστούν και οι δυο. Αν το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο ή ίσο της μεγαλύτερης βάσης, τότε θα είναι και της μικρότερης. Οπότε, όχι, δε μιλάμε για το άθροισμα των βάσεων.- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ανισότητα σε τραπέζιο
Σ' ευχαριστώ Αλέξανδρε για την διευκρίνιση.Al.Koutsouridis έγραψε: ↑Σάβ Δεκ 19, 2020 5:59 pmΚαλησπέρα!
Εφόσον δεν διευκρινίζεται στην εκφώνηση για για ποιά από τις δυο γωνίες είναι, θα πρέπει να εξεταστούν και οι δυο. Αν το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο ή ίσο της μεγαλύτερης βάσης, τότε θα είναι και της μικρότερης. Οπότε, όχι, δε μιλάμε για το άθροισμα των βάσεων.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Γιώργο όχι ακριβώς, στην περίπτωση που η γωνία τωνgeorge visvikis έγραψε: ↑Σάβ Δεκ 19, 2020 5:24 pmΚαλησπέρα σε όλους!
Νομίζω ότι πρώτα πρέπει να ξεκαθαρίσουμε (επειδή η εκφώνηση δεν είναι σαφής) ότι η γωνία τωνείναι εκείνη που βαίνει στις βάσεις και όχι στις μη παράλληλες πλευρές, όπου έχουμε το ακριβώς αντίθετο αποτέλεσμα. Υποθέτω επίσης ότι μιλάμε για το άθροισμα των βάσεων.
 δεν είναι εκείνη που βαίνει στις βάσεις (όπως ενστικτωδώς και αυθαιρέτως υπέθεσα) αλλά εκείνη που βαίνει στις μη παράλληλες πλευρές ... μπορεί το άθροισμα των μη παραλλήλων πλευρών να είναι είτε μικρότερο είτε μεγαλύτερο του αθροίσματος των βάσεων: στο σχήμα του συνημμένου για παράδειγμα, έχουμε (από Πυθαγόρειο Θεώρημα και Νόμο Συνημιτόνων)
δεν είναι εκείνη που βαίνει στις βάσεις (όπως ενστικτωδώς και αυθαιρέτως υπέθεσα) αλλά εκείνη που βαίνει στις μη παράλληλες πλευρές ... μπορεί το άθροισμα των μη παραλλήλων πλευρών να είναι είτε μικρότερο είτε μεγαλύτερο του αθροίσματος των βάσεων: στο σχήμα του συνημμένου για παράδειγμα, έχουμε (από Πυθαγόρειο Θεώρημα και Νόμο Συνημιτόνων)  αλλά επίσης (εκφυλισμένο τραπέζιο, τριγωνική ανισότητα)
αλλά επίσης (εκφυλισμένο τραπέζιο, τριγωνική ανισότητα)  .
.Οπότε: αν
 ,
,  οι βάσεις τραπεζίου και
οι βάσεις τραπεζίου και  η τομή των διαγωνίων
η τομή των διαγωνίων  ,
,  με
με  τότε ΝΑΙ, ισχύει η
τότε ΝΑΙ, ισχύει η  (ενδεχομένως και με κάποια βελτίωση*)^ αν
(ενδεχομένως και με κάποια βελτίωση*)^ αν  τότε άλλοτε ισχύει η
τότε άλλοτε ισχύει η  και άλλοτε ισχύει η
και άλλοτε ισχύει η  .
.*να βρεθεί δηλαδή ελάχιστη σταθερά
 ώστε, με τις ίδιες υποθέσεις, να ισχύει η
ώστε, με τις ίδιες υποθέσεις, να ισχύει η 
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Δεν μπορεί να βελτιωθεί το
 ... όπως ξεκάθαρα μας δείχνει η ειδική περίπτωση του παραλληλογράμμου
... όπως ξεκάθαρα μας δείχνει η ειδική περίπτωση του παραλληλογράμμου Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Ας δώσουμε άνω και κάτω φράγματα για τον λόγο  , όπου
, όπου  οι παράλληλες πλευρές τραπεζίου
οι παράλληλες πλευρές τραπεζίου  του οποίου οι διαγώνιοι τέμνονται κατά γωνία βαίνουσα προς τις
του οποίου οι διαγώνιοι τέμνονται κατά γωνία βαίνουσα προς τις  ίση προς γωνία
ίση προς γωνία  , όπου
, όπου  . Αυτό θα γίνει με την βοήθεια ενός 'γενεσιακού' (generic) τραπεζίου/τριγώνου όπως στο συνημμένο: προκύπτουν ουσιαστικά όλα τα τραπέζια ως τριπαραμετρική οικογένεια με παραμέτρους
. Αυτό θα γίνει με την βοήθεια ενός 'γενεσιακού' (generic) τραπεζίου/τριγώνου όπως στο συνημμένο: προκύπτουν ουσιαστικά όλα τα τραπέζια ως τριπαραμετρική οικογένεια με παραμέτρους  ,
,  και
και  , όπου
, όπου  ,
,  . Καταλήγουμε στην ανισότητα
. Καταλήγουμε στην ανισότητα

λόγω της ανισότητας (που προκύπτει σχετικά εύκολα με πράξεις)

Οι τρεις παράμετροι γίνονται λοιπόν δύο, και το μόνο που απομένει είναι η μεγιστοποίηση της και η ελαχιστοποίηση της
και η ελαχιστοποίηση της  , για
, για  . (Κρατάμε την γωνία
. (Κρατάμε την γωνία  των διαγωνίων σταθερή ... σύμφωνα με το αρχικό πρόβλημα.)
των διαγωνίων σταθερή ... σύμφωνα με το αρχικό πρόβλημα.)
Η παράγωγος του τετραγώνου της ισούται προς
ισούται προς  , συνεπώς ισχύει η
, συνεπώς ισχύει η
 για
για  και
και  .
.
Η παράγωγος του τετραγώνου της ισούται προς
ισούται προς  : συμπεραίνουμε ότι η
: συμπεραίνουμε ότι η  ελαχιστοποιείται για
ελαχιστοποιείται για  όταν
όταν  αλλά για
αλλά για  όταν
όταν  , ισχύουν δηλαδή οι
, ισχύουν δηλαδή οι
 για
για  και
και 
και
 για
για  και
και 
Καταλήγουμε στις ανισότητες
 για
για 
και
 για
για 
 , όπου
, όπου  οι παράλληλες πλευρές τραπεζίου
οι παράλληλες πλευρές τραπεζίου  του οποίου οι διαγώνιοι τέμνονται κατά γωνία βαίνουσα προς τις
του οποίου οι διαγώνιοι τέμνονται κατά γωνία βαίνουσα προς τις  ίση προς γωνία
ίση προς γωνία  , όπου
, όπου  . Αυτό θα γίνει με την βοήθεια ενός 'γενεσιακού' (generic) τραπεζίου/τριγώνου όπως στο συνημμένο: προκύπτουν ουσιαστικά όλα τα τραπέζια ως τριπαραμετρική οικογένεια με παραμέτρους
. Αυτό θα γίνει με την βοήθεια ενός 'γενεσιακού' (generic) τραπεζίου/τριγώνου όπως στο συνημμένο: προκύπτουν ουσιαστικά όλα τα τραπέζια ως τριπαραμετρική οικογένεια με παραμέτρους  ,
,  και
και  , όπου
, όπου  ,
,  . Καταλήγουμε στην ανισότητα
. Καταλήγουμε στην ανισότητα
λόγω της ανισότητας (που προκύπτει σχετικά εύκολα με πράξεις)

Οι τρεις παράμετροι γίνονται λοιπόν δύο, και το μόνο που απομένει είναι η μεγιστοποίηση της
 και η ελαχιστοποίηση της
και η ελαχιστοποίηση της  , για
, για  . (Κρατάμε την γωνία
. (Κρατάμε την γωνία  των διαγωνίων σταθερή ... σύμφωνα με το αρχικό πρόβλημα.)
των διαγωνίων σταθερή ... σύμφωνα με το αρχικό πρόβλημα.)Η παράγωγος του τετραγώνου της
 ισούται προς
ισούται προς  , συνεπώς ισχύει η
, συνεπώς ισχύει η  για
για  και
και  .
.Η παράγωγος του τετραγώνου της
 ισούται προς
ισούται προς  : συμπεραίνουμε ότι η
: συμπεραίνουμε ότι η  ελαχιστοποιείται για
ελαχιστοποιείται για  όταν
όταν  αλλά για
αλλά για  όταν
όταν  , ισχύουν δηλαδή οι
, ισχύουν δηλαδή οι  για
για  και
και 
και
 για
για  και
και 
Καταλήγουμε στις ανισότητες
 για
για 
και
 για
για 
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ανισότητα σε τραπέζιο
Να ευχαριστήσουμε τον λ.Μπαλόγλου για την μελέτη και λύση του γενικότερου προβλήματος.
Για την συνοχή του νήματος ας δούμε και την λύση εντός φακέλου:
 το τραπέζιο,
το τραπέζιο,  η μεγαλύτερη βάση του και
η μεγαλύτερη βάση του και  το σημείο τομής των διαγωνίων του. Αρκεί να δείξουμε οτι το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο από την μεγαλύτερη βάση του τραπεζίου, τότε θα είναι και από την μικρότερη. Διακρίνουμε δυο περιπτώσεις:
το σημείο τομής των διαγωνίων του. Αρκεί να δείξουμε οτι το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο από την μεγαλύτερη βάση του τραπεζίου, τότε θα είναι και από την μικρότερη. Διακρίνουμε δυο περιπτώσεις:
Οι γωνίες είναι ίσες με
είναι ίσες με  . Επειδή απέναντι από την μεγαλύτερη γωνία βρίσκεται η μεγαλύτερη πλευρά του τριγώνου
. Επειδή απέναντι από την μεγαλύτερη γωνία βρίσκεται η μεγαλύτερη πλευρά του τριγώνου  , θα έχουμε
, θα έχουμε  και αντίστοιχα στο τρίγωνο
και αντίστοιχα στο τρίγωνο  ,
,  . Προσθέτoντας κατά μέλη τις παραπάνω ανισώσεις έχουμε
. Προσθέτoντας κατά μέλη τις παραπάνω ανισώσεις έχουμε  . Η τελευταία, λόγω της τριγωνικής ανισότητας στο
. Η τελευταία, λόγω της τριγωνικής ανισότητας στο  .
.
Οι γωνίες είναι ίσες με
είναι ίσες με  . Σε αυτήν την περίπτωση φέρουμε την διχοτόμο της γωνίας
. Σε αυτήν την περίπτωση φέρουμε την διχοτόμο της γωνίας  , έστω
, έστω  σημείο αυτής προς την πλευρά της μεγαλύτερης βάσης τέτοιο, ώστε
σημείο αυτής προς την πλευρά της μεγαλύτερης βάσης τέτοιο, ώστε  και αντίστοιχα σημείο
και αντίστοιχα σημείο  , ώστε
, ώστε  . Τότε θα ισχύει
. Τότε θα ισχύει
 και επειδή
και επειδή  , τα τρίγωνα
, τα τρίγωνα  και
και  είναι όμοια.
είναι όμοια.
Άρα και .
.
Αν , τότε
, τότε  . (
. ( από την κατασκευή μας τα σημεία
από την κατασκευή μας τα σημεία  είναι συμμετρικά ως προς την
είναι συμμετρικά ως προς την  και αντίστοιχα τα
και αντίστοιχα τα  ως προς την
ως προς την 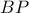 ). Επομένως θα έχουμε
). Επομένως θα έχουμε
 .
.
Αν , τότε
, τότε  και άρα θα έχουμε
και άρα θα έχουμε
 .
.
Σε όλες τις περιπτώσεις λοιπόν, το ζητούμενο ισχύει.
Για την συνοχή του νήματος ας δούμε και την λύση εντός φακέλου:
Έστωέγραψε: ↑Παρ Δεκ 18, 2020 11:08 pmΟι διαγώνιοι ενός τραπεζίου τέμνονται υπό γωνία. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
 το τραπέζιο,
το τραπέζιο,  η μεγαλύτερη βάση του και
η μεγαλύτερη βάση του και  το σημείο τομής των διαγωνίων του. Αρκεί να δείξουμε οτι το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο από την μεγαλύτερη βάση του τραπεζίου, τότε θα είναι και από την μικρότερη. Διακρίνουμε δυο περιπτώσεις:
το σημείο τομής των διαγωνίων του. Αρκεί να δείξουμε οτι το άθροισμα των μη παράλληλων πλευρών είναι μεγαλύτερο από την μεγαλύτερη βάση του τραπεζίου, τότε θα είναι και από την μικρότερη. Διακρίνουμε δυο περιπτώσεις:Οι γωνίες
 είναι ίσες με
είναι ίσες με  . Επειδή απέναντι από την μεγαλύτερη γωνία βρίσκεται η μεγαλύτερη πλευρά του τριγώνου
. Επειδή απέναντι από την μεγαλύτερη γωνία βρίσκεται η μεγαλύτερη πλευρά του τριγώνου  , θα έχουμε
, θα έχουμε  και αντίστοιχα στο τρίγωνο
και αντίστοιχα στο τρίγωνο  ,
,  . Προσθέτoντας κατά μέλη τις παραπάνω ανισώσεις έχουμε
. Προσθέτoντας κατά μέλη τις παραπάνω ανισώσεις έχουμε  . Η τελευταία, λόγω της τριγωνικής ανισότητας στο
. Η τελευταία, λόγω της τριγωνικής ανισότητας στο  .
.Οι γωνίες
 είναι ίσες με
είναι ίσες με  . Σε αυτήν την περίπτωση φέρουμε την διχοτόμο της γωνίας
. Σε αυτήν την περίπτωση φέρουμε την διχοτόμο της γωνίας  , έστω
, έστω  σημείο αυτής προς την πλευρά της μεγαλύτερης βάσης τέτοιο, ώστε
σημείο αυτής προς την πλευρά της μεγαλύτερης βάσης τέτοιο, ώστε  και αντίστοιχα σημείο
και αντίστοιχα σημείο  , ώστε
, ώστε  . Τότε θα ισχύει
. Τότε θα ισχύει  και επειδή
και επειδή  , τα τρίγωνα
, τα τρίγωνα  και
και  είναι όμοια.
είναι όμοια.Άρα και
 .
.Αν
 , τότε
, τότε  . (
. ( από την κατασκευή μας τα σημεία
από την κατασκευή μας τα σημεία  είναι συμμετρικά ως προς την
είναι συμμετρικά ως προς την  και αντίστοιχα τα
και αντίστοιχα τα  ως προς την
ως προς την 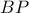 ). Επομένως θα έχουμε
). Επομένως θα έχουμε .
.Αν
 , τότε
, τότε  και άρα θα έχουμε
και άρα θα έχουμε .
.Σε όλες τις περιπτώσεις λοιπόν, το ζητούμενο ισχύει.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Δηλαδή Αλέξανδρε ... και εκτός φακέλου και εκτός θέματος βρέθηκα;!Al.Koutsouridis έγραψε: ↑Πέμ Δεκ 24, 2020 11:49 amΝα ευχαριστήσουμε τον λ.Μπαλόγλου για την μελέτη και λύση του γενικότερου προβλήματος.
Για την συνοχή του νήματος ας δούμε και την λύση εντός φακέλου:
έγραψε: ↑Παρ Δεκ 18, 2020 11:08 pmΟι διαγώνιοι ενός τραπεζίου τέμνονται υπό γωνία. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.
Λοιπόν ... ψυχραιμία: οι μεν ανισότητες που χρησιμοποίησα αποδεικνύονται εύκολα και χωρίς παραγώγους, το δε πρόβλημα όντως ζητούσε το άθροισμα των μη παραλήλων πλευρών να υπερβαίνει την μεγαλύτερη βάση, κάτι που σχετικά εύκολα αποδεικνύεται ΚΑΙ αλγεβρικά όταν η γωνία που βαίνει στις παράλληλες πλευρές είναι οξεία, και ΜΑΛΛΟΝ ισχύει και όταν είναι αμβλεία (ΟΧΙ υποχρεωτικά
 ), αναγόμενο συγκεκριμένα (και σύμφωνα με την παραπάνω μέθοδο μου πάντοτε) στην ανισότητα τριών μεταβλητών
), αναγόμενο συγκεκριμένα (και σύμφωνα με την παραπάνω μέθοδο μου πάντοτε) στην ανισότητα τριών μεταβλητών
Η ανισότητα αυτή φαίνεται ότι όντως ισχύει για
 ,
,  ,
,  , αλλά δεν έχω ακόμη απόδειξη: την καταθέτω εδώ με σκοπό να την αποδείξω κάποτε, ενθαρρύνοντας ταυτόχρονα άλλους είτε να την παλέψουν είτε να προσπαθήσουν γεωμετρικά για ΤΥΧΟΥΣΑ αμβλεία γωνία διαγωνίων!
, αλλά δεν έχω ακόμη απόδειξη: την καταθέτω εδώ με σκοπό να την αποδείξω κάποτε, ενθαρρύνοντας ταυτόχρονα άλλους είτε να την παλέψουν είτε να προσπαθήσουν γεωμετρικά για ΤΥΧΟΥΣΑ αμβλεία γωνία διαγωνίων!ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1 μμ: διορθώθηκε το δεξιό σκέλος της παραπάνω ανισότητας (τετραγωνική ρίζα και αλλαγή προσήμου).
τελευταία επεξεργασία από gbaloglou σε Παρ Δεκ 25, 2020 1:07 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Όχι βέβαια, δεν μπορεί να ισχύει για τυχούσα γωνία διαγωνίων, ας σκεφθούμε πχ ένα επίμηκες ορθογώνιο όπουgbaloglou έγραψε: ↑Πέμ Δεκ 24, 2020 11:38 pmΔηλαδή Αλέξανδρε ... και εκτός φακέλου και εκτός θέματος βρέθηκα;!Al.Koutsouridis έγραψε: ↑Πέμ Δεκ 24, 2020 11:49 amΝα ευχαριστήσουμε τον λ.Μπαλόγλου για την μελέτη και λύση του γενικότερου προβλήματος.
Για την συνοχή του νήματος ας δούμε και την λύση εντός φακέλου:
έγραψε: ↑Παρ Δεκ 18, 2020 11:08 pmΟι διαγώνιοι ενός τραπεζίου τέμνονται υπό γωνία. Να αποδείξετε ότι το άθροισμα των μη παράλληλων πλευρών του είναι μεγαλύτερο ή ίσο από τις βάσεις του.

Λοιπόν ... ψυχραιμία: οι μεν ανισότητες που χρησιμοποίησα αποδεικνύονται εύκολα και χωρίς παραγώγους, το δε πρόβλημα όντως ζητούσε το άθροισμα των μη παραλήλων πλευρών να υπερβαίνει την μεγαλύτερη βάση, κάτι που σχετικά εύκολα αποδεικνύεται ΚΑΙ αλγεβρικά όταν η γωνία που βαίνει στις παράλληλες πλευρές είναι οξεία, και ΜΑΛΛΟΝ ισχύει και όταν είναι αμβλεία (ΟΧΙ υποχρεωτικά), αναγόμενο συγκεκριμένα (και σύμφωνα με την παραπάνω μέθοδο μου πάντοτε) στην ανισότητα τριών μεταβλητών
Η ανισότητα αυτή φαίνεται ότι όντως ισχύει για,
,
, αλλά δεν έχω ακόμη απόδειξη: την καταθέτω εδώ με σκοπό να την αποδείξω κάποτε, ενθαρρύνοντας ταυτόχρονα άλλους είτε να την παλέψουν είτε να προσπαθήσουν γεωμετρικά για ΤΥΧΟΥΣΑ αμβλεία γωνία διαγωνίων!
 και
και  , οπότε το δεξιό σκέλος είναι περίπου
, οπότε το δεξιό σκέλος είναι περίπου  και το αριστερό σκέλος περίπου
και το αριστερό σκέλος περίπου  .
.ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1:20 μμ: έγινε διόρθωση στο δεξιό σκέλος της ανισότητας (κατά την αμέσως προηγούμενη δημοσίευση) και διεγράφη άτοπη αλγεβρική απόδειξη (για
 ) -- η προσπάθεια συνεχίζεται!
) -- η προσπάθεια συνεχίζεται!Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ανισότητα σε τραπέζιο
Καλησπέρα κ.Γιώργο και χρόνια πολλά!gbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 9:42 am
Όχι βέβαια, δεν μπορεί να ισχύει για τυχούσα γωνία διαγωνίων, ας σκεφθούμε πχ ένα επίμηκες ορθογώνιο όπουκαι
, οπότε το δεξιό σκέλος είναι περίπου
και το αριστερό σκέλος περίπου
.
ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1:20 μμ: έγινε διόρθωση στο δεξιό σκέλος της ανισότητας (κατά την αμέσως προηγούμενη δημοσίευση) και διεγράφη άτοπη αλγεβρική απόδειξη (για) -- η προσπάθεια συνεχίζεται!
Ίσως ενδιαφέρον θα ήταν να το δούμε για
 . Δεν το έχω εξετάσει είναι η αλήθεια όμως.
. Δεν το έχω εξετάσει είναι η αλήθεια όμως.- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Αλέξανδρε σχεδόν σίγουρα ισχύει απόAl.Koutsouridis έγραψε: ↑Παρ Δεκ 25, 2020 5:07 pmgbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 9:42 am
Όχι βέβαια, δεν μπορεί να ισχύει για τυχούσα γωνία διαγωνίων, ας σκεφθούμε πχ ένα επίμηκες ορθογώνιο όπουκαι
, οπότε το δεξιό σκέλος είναι περίπου
και το αριστερό σκέλος περίπου
.
ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1:20 μμ: έγινε διόρθωση στο δεξιό σκέλος της ανισότητας (κατά την αμέσως προηγούμενη δημοσίευση) και διεγράφη άτοπη αλγεβρική απόδειξη (για) -- η προσπάθεια συνεχίζεται!
Καλησπέρα κ.Γιώργο και χρόνια πολλά!
Ίσως ενδιαφέρον θα ήταν να το δούμε για. Δεν το έχω εξετάσει είναι η αλήθεια όμως.
 (όπως 'υποδεικνύει' το συνημμένο) και κάτω (όπως προκύπτει από την παρακάτω παραγώγιση ως προς την γωνία
(όπως 'υποδεικνύει' το συνημμένο) και κάτω (όπως προκύπτει από την παρακάτω παραγώγιση ως προς την γωνία  ):
):

Προς το παρόν ... έχοντας γεωμετρική απόδειξη για
 ... μπορούμε άμεσα να κατηφορήσουμε ως το
... μπορούμε άμεσα να κατηφορήσουμε ως το  ... χάρις στην παραπάνω παρατηρηθείσα μονοτονία! (Στην πραγματικότητα μπορούμε να κατέβουμε ως το
... χάρις στην παραπάνω παρατηρηθείσα μονοτονία! (Στην πραγματικότητα μπορούμε να κατέβουμε ως το  , αλλά εδώ δεν χρειαζόμαστε την μονοτονία, μια και ήδη γνωρίζουμε την ισχύ της ανισότητας για οξείες γωνίες
, αλλά εδώ δεν χρειαζόμαστε την μονοτονία, μια και ήδη γνωρίζουμε την ισχύ της ανισότητας για οξείες γωνίες  .)
.)Όσον αφορά τις γωνίες μεταξύ
 και
και  ή/και αλγεβρική απόδειξη ... θα προτιμούσα να (προσπαθήσω να) συνδυάσω αυτά τα δύο, δίνοντας πρώτα αλγεβρική απόδειξη για την γωνία
ή/και αλγεβρική απόδειξη ... θα προτιμούσα να (προσπαθήσω να) συνδυάσω αυτά τα δύο, δίνοντας πρώτα αλγεβρική απόδειξη για την γωνία  [δύσκολο] και ακολούθως κατεβαίνοντας όπως παραπάνω [άμεσο]. Παραθέτω εδώ την επιθυμητή ανισότητα,
[δύσκολο] και ακολούθως κατεβαίνοντας όπως παραπάνω [άμεσο]. Παραθέτω εδώ την επιθυμητή ανισότητα,
KAI μία ισοδύναμη προς αυτήν ανισότητα (για
 ,
,  πάντοτε):
πάντοτε):

Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Και όμως ΔΕΝ ισχύει η προταθείσα παραπάνω ανισότητα, καθώς γιαgbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 11:43 pmΑλέξανδρε σχεδόν σίγουρα ισχύει απόAl.Koutsouridis έγραψε: ↑Παρ Δεκ 25, 2020 5:07 pmgbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 9:42 am
Όχι βέβαια, δεν μπορεί να ισχύει για τυχούσα γωνία διαγωνίων, ας σκεφθούμε πχ ένα επίμηκες ορθογώνιο όπουκαι
, οπότε το δεξιό σκέλος είναι περίπου
και το αριστερό σκέλος περίπου
.
ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1:20 μμ: έγινε διόρθωση στο δεξιό σκέλος της ανισότητας (κατά την αμέσως προηγούμενη δημοσίευση) και διεγράφη άτοπη αλγεβρική απόδειξη (για) -- η προσπάθεια συνεχίζεται!
Καλησπέρα κ.Γιώργο και χρόνια πολλά!
Ίσως ενδιαφέρον θα ήταν να το δούμε για. Δεν το έχω εξετάσει είναι η αλήθεια όμως.
(όπως 'υποδεικνύει' το συνημμένο) και κάτω (όπως προκύπτει από την παρακάτω παραγώγιση ως προς την γωνία
):
Προς το παρόν ... έχοντας γεωμετρική απόδειξη για... μπορούμε άμεσα να κατηφορήσουμε ως το
... χάρις στην παραπάνω παρατηρηθείσα μονοτονία! (Στην πραγματικότητα μπορούμε να κατέβουμε ως το
, αλλά εδώ δεν χρειαζόμαστε την μονοτονία, μια και ήδη γνωρίζουμε την ισχύ της ανισότητας για οξείες γωνίες
.)
Όσον αφορά τις γωνίες μεταξύκαι
ή/και αλγεβρική απόδειξη ... θα προτιμούσα να (προσπαθήσω να) συνδυάσω αυτά τα δύο, δίνοντας πρώτα αλγεβρική απόδειξη για την γωνία
[δύσκολο] και ακολούθως κατεβαίνοντας όπως παραπάνω [άμεσο]. Παραθέτω εδώ την επιθυμητή ανισότητα,
KAI μία ισοδύναμη προς αυτήν ανισότητα (για,
πάντοτε):
 ,
,  ... το αριστερό σκέλος (
... το αριστερό σκέλος ( ) ισούται προς
) ισούται προς  , ενώ το δεξιό σκέλος (
, ενώ το δεξιό σκέλος ( ) ισούται προς
) ισούται προς  !
!Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Το παραπάνω αντιπαράδειγμα μού το βρήκε το WolframAlpha, ΚΑΚΩΣ όμως κατέφυγα εκεί: η ίδια η Γεωμετρία, και πιο συγκεκριμένα το ίδιο το παράδειγμα που χρησιμοποίησα για να βάλω την γωνίαgbaloglou έγραψε: ↑Σάβ Δεκ 26, 2020 1:26 amΚαι όμως ΔΕΝ ισχύει η προταθείσα παραπάνω ανισότητα, καθώς γιαgbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 11:43 pmΑλέξανδρε σχεδόν σίγουρα ισχύει απόAl.Koutsouridis έγραψε: ↑Παρ Δεκ 25, 2020 5:07 pmgbaloglou έγραψε: ↑Παρ Δεκ 25, 2020 9:42 am
Όχι βέβαια, δεν μπορεί να ισχύει για τυχούσα γωνία διαγωνίων, ας σκεφθούμε πχ ένα επίμηκες ορθογώνιο όπουκαι
, οπότε το δεξιό σκέλος είναι περίπου
και το αριστερό σκέλος περίπου
.
ΕΠΕΞΕΡΓΑΣΙΑ 25-12-2020 1:20 μμ: έγινε διόρθωση στο δεξιό σκέλος της ανισότητας (κατά την αμέσως προηγούμενη δημοσίευση) και διεγράφη άτοπη αλγεβρική απόδειξη (για) -- η προσπάθεια συνεχίζεται!
Καλησπέρα κ.Γιώργο και χρόνια πολλά!
Ίσως ενδιαφέρον θα ήταν να το δούμε για. Δεν το έχω εξετάσει είναι η αλήθεια όμως.
(όπως 'υποδεικνύει' το συνημμένο) και κάτω (όπως προκύπτει από την παρακάτω παραγώγιση ως προς την γωνία
):
Προς το παρόν ... έχοντας γεωμετρική απόδειξη για... μπορούμε άμεσα να κατηφορήσουμε ως το
... χάρις στην παραπάνω παρατηρηθείσα μονοτονία! (Στην πραγματικότητα μπορούμε να κατέβουμε ως το
, αλλά εδώ δεν χρειαζόμαστε την μονοτονία, μια και ήδη γνωρίζουμε την ισχύ της ανισότητας για οξείες γωνίες
.)
Όσον αφορά τις γωνίες μεταξύκαι
ή/και αλγεβρική απόδειξη ... θα προτιμούσα να (προσπαθήσω να) συνδυάσω αυτά τα δύο, δίνοντας πρώτα αλγεβρική απόδειξη για την γωνία
[δύσκολο] και ακολούθως κατεβαίνοντας όπως παραπάνω [άμεσο]. Παραθέτω εδώ την επιθυμητή ανισότητα,
KAI μία ισοδύναμη προς αυτήν ανισότητα (για,
πάντοτε):
,
... το αριστερό σκέλος (
) ισούται προς
, ενώ το δεξιό σκέλος (
) ισούται προς
!
 στο παιγνίδι ... εξηγούν (κόκκινο τραπέζιο) γιατί η γωνία αυτή ΔΕΝ εγγυάται την υπέρβαση του αθροίσματος των μη παραλλήλων πλευρών έναντι της μεγαλύτερης βάσης ... ΚΑΙ ταυτόχρονα γιατί ΚΑΜΙΑ άλλη γωνία διαγωνίων μεγαλύτερη των
στο παιγνίδι ... εξηγούν (κόκκινο τραπέζιο) γιατί η γωνία αυτή ΔΕΝ εγγυάται την υπέρβαση του αθροίσματος των μη παραλλήλων πλευρών έναντι της μεγαλύτερης βάσης ... ΚΑΙ ταυτόχρονα γιατί ΚΑΜΙΑ άλλη γωνία διαγωνίων μεγαλύτερη των  δεν εγγυάται την εν λόγω υπέρβαση! (Στο παρακάτω σχήμα όντως
δεν εγγυάται την εν λόγω υπέρβαση! (Στο παρακάτω σχήμα όντως  .)
.)Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
gbaloglou έγραψε: ↑Σάβ Δεκ 26, 2020 8:15 amΌσον αφορά τις γωνίες μεταξύκαι
ή/και αλγεβρική απόδειξη ... θα προτιμούσα να (προσπαθήσω να) συνδυάσω αυτά τα δύο, δίνοντας πρώτα αλγεβρική απόδειξη για την γωνία
[δύσκολο] και ακολούθως κατεβαίνοντας όπως παραπάνω [άμεσο]. Παραθέτω εδώ την επιθυμητή ανισότητα,
KAI μία ισοδύναμη προς αυτήν ανισότητα (για,
πάντοτε):
ΙΣΧΥΕΙ πάντως η επιθυμητή γεωμετρική ανισότητα γιαΚαι όμως ΔΕΝ ισχύει η προταθείσα παραπάνω ανισότητα, καθώς για,
... το αριστερό σκέλος (
) ισούται προς
, ενώ το δεξιό σκέλος (
) ισούται προς
!
 -- αλλά ούτε λεπτό παραπάνω -- και έχουμε γι αυτό την εξαιρετικής τεχνοτροπίας απόδειξη που παρέθεσε ο Αλέξανδρος. Αν το αλγεβροποιήσουμε το θέμα, η επιθυμητή ανισότητα λαμβάνει, όπως είδαμε, την μορφή
-- αλλά ούτε λεπτό παραπάνω -- και έχουμε γι αυτό την εξαιρετικής τεχνοτροπίας απόδειξη που παρέθεσε ο Αλέξανδρος. Αν το αλγεβροποιήσουμε το θέμα, η επιθυμητή ανισότητα λαμβάνει, όπως είδαμε, την μορφή
που ύστερα από αρκετές πράξεις λαμβάνει την μορφή


Η ανισότητα αυτή ΙΣΧΥΕΙ για
 ,
,  -- ως ισότητα για
-- ως ισότητα για  (ευθύγραμμο τμήμα) και για
(ευθύγραμμο τμήμα) και για  (εξ ορθογωνίου παραλληλογράμμου τραπέζιο όπως στην προηγούμενη δημοσίευση) -- αλλά δεν έχω ως τώρα βρει τρόπο απόδειξης.
(εξ ορθογωνίου παραλληλογράμμου τραπέζιο όπως στην προηγούμενη δημοσίευση) -- αλλά δεν έχω ως τώρα βρει τρόπο απόδειξης.Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα σε τραπέζιο
Η ανισότητα ισχύει ως ισοδύναμη της προφανώς ισχύουσαςgbaloglou έγραψε: ↑Δευ Δεκ 28, 2020 12:12 amΙΣΧΥΕΙ πάντως η επιθυμητή γεωμετρική ανισότητα για-- αλλά ούτε λεπτό παραπάνω -- και έχουμε γι αυτό την εξαιρετικής τεχνοτροπίας απόδειξη που παρέθεσε ο Αλέξανδρος. Αν το αλγεβροποιήσουμε το θέμα, η επιθυμητή ανισότητα λαμβάνει, όπως είδαμε, την μορφή
που ύστερα από αρκετές πράξεις λαμβάνει την μορφή
Η ανισότητα αυτή ΙΣΧΥΕΙ για,
-- ως ισότητα για
(ευθύγραμμο τμήμα) και για
(εξ ορθογωνίου παραλληλογράμμου τραπέζιο όπως στην προηγούμενη δημοσίευση) -- αλλά δεν έχω ως τώρα βρει τρόπο απόδειξης.

Ισότητα μπορεί να ισχύει μόνον όταν είτε
 , οπότε επίσης
, οπότε επίσης  , είτε
, είτε  , οπότε επίσης
, οπότε επίσης  .
.Η περίπτωση
 είναι τετριμμένη (ευθύγραμμο τμήμα), ενώ η περίπτωση
είναι τετριμμένη (ευθύγραμμο τμήμα), ενώ η περίπτωση  αντιστοιχεί σε τραπέζιο με τρεις ίσες πλευρές:
αντιστοιχεί σε τραπέζιο με τρεις ίσες πλευρές:Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες

