Ισεμβαδικότητα για νευρικούς

KARKAR · #1

: Ισεμβαδικότητα για νευρικούς.png (19.28 KiB) Προβλήθηκε 467 φορές

Οι κύκλοι (O)

και

είναι ίσοι και εφάπτονται εξωτερικά στο

, ενώ

ονομάσαμε

το αντιδιαμετρικό του

στον

. Από σημείο

της

φέρουμε εφαπτομένη

προς

τον (K)

, η οποία τέμνει τον (O)

στο

. Για ποια θέση του

, είναι :

;

#2

KARKAR έγραψε: ↑
Τετ Οκτ 28, 2020 1:42 pm
Ισεμβαδικότητα για νευρικούς.pngΟι κύκλοι και είναι ίσοι και εφάπτονται εξωτερικά στο , ενώ ονομάσαμε

το αντιδιαμετρικό του στον . Από σημείο της φέρουμε εφαπτομένη προς

τον , η οποία τέμνει τον στο . Για ποια θέση του , είναι : ;

: Για νευρικούς.png (22.2 KiB) Προβλήθηκε 442 φορές

Όντως για νευρικούς. Τόσο νευρικός ούτε ο Γούντι Άλεν στην ταινία "ο νευρικός εραστής"

$\displaystyle OS = \frac{{11R}}{{25}}$

Edit: Άρση απόκρυψης.

#3

KARKAR έγραψε: ↑
Τετ Οκτ 28, 2020 1:42 pm
Ισεμβαδικότητα για νευρικούς.pngΟι κύκλοι και είναι ίσοι και εφάπτονται εξωτερικά στο , ενώ ονομάσαμε

το αντιδιαμετρικό του στον . Από σημείο της φέρουμε εφαπτομένη προς

τον , η οποία τέμνει τον στο . Για ποια θέση του , είναι : ;

Ανάλυση:

Έστω λυμένο το πρόβλημα και ας είναι PH = h

το ύψος του $\vartriangle PAS$ .

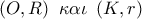Θεωρώ γνωστό ότι : Αν οι κύκλοι , $\left( {O,R} \right)\,\,\kappa \alpha \iota \,\,\left( {K,r} \right)$ τέμνονται στα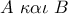 $A\,\,\kappa \alpha \iota \,\,B$

Για το εφαπτόμενο τμήμα , έστω

από τυχαίο σημείο

του πρώτου προς τον δεύτερο ισχύει:

$\boxed{\dfrac{{PA \cdot PB}}{{{x^2}}} = \dfrac{R}{d}}\,\,$ . Το

είναι η διάκεντρος ενώ PT = x

.

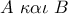Οριακά εδώ τα $A\,\,\kappa \alpha \iota \,\,B$ ταυτίζονται και άρα με PB = m

έχω: $\dfrac{{{m^2}}}{{{x^2}}} = \dfrac{R}{{2R}} = \dfrac{1}{2}\,\,\left( 1 \right)$

: Εμβαδόν για νευρικούς_κατασκευή.png (38.12 KiB) Προβλήθηκε 395 φορές

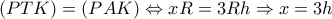Επειδή : $\left( {PTK} \right) = \left( {PAK} \right) \Leftrightarrow xR = 3Rh \Rightarrow x = 3h$ και έτσι η $\left( 1 \right)$ δίδει:

$\dfrac{m}{h} = \dfrac{3}{{\sqrt 2 }} = \dfrac{{2R}}{{AP}} \Rightarrow \boxed{AP = \dfrac{{2R\sqrt 2 }}{3}}$

Κατασκευή :

Αν φέρω κάθετη στο

επί την

και κόψει π. χ. το κάτω ημικύκλιο στο

Ο κύκλος $\left( {A,\dfrac{{2AF}}{3}} \right)$ τέμνει το πάνω ημικύκλιο στο

και φέρνω μετά το εφαπτόμενο τμήμα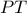

προς τον κύκλο $\left( {K,R} \right)$

Παρατήρηση: Το τετράπλευρο , είναι τραπέζιο .

Ισεμβαδικότητα για νευρικούς

Ισεμβαδικότητα για νευρικούς

Re: Ισεμβαδικότητα για νευρικούς

Re: Ισεμβαδικότητα για νευρικούς

Μέλη σε σύνδεση