Σελίδα 1 από 1
Με απλά "μέσα"
Δημοσιεύτηκε: Κυρ Ιουν 28, 2020 12:28 am
από ΔΗΜΗΤΡΗΣ ΚΟΛΤΣΗΣ
Δίνεται οξυγώνιο τρίγωνο

, με

και έστω

ο περιγεγραμμένος του κύκλος.
Φέρουμε τα ύψη

και
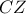
. Ες είναι

ένα τυχαίο σημείο του μικρού τόξου

. Οι ευθείες

και
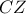
τέμνονται στο

, ενώ οι

και

στο

. Τέλος , αν

το συμμετρικό του

ως προς το

, να αποδείξετε ότι

.
Re: Με απλά "μέσα"
Δημοσιεύτηκε: Κυρ Ιουν 28, 2020 1:02 am
από ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
ΔΗΜΗΤΡΗΣ ΚΟΛΤΣΗΣ έγραψε: ↑Κυρ Ιουν 28, 2020 12:28 am
Δίνεται οξυγώνιο τρίγωνο

, με

και έστω

ο περιγεγραμμένος του κύκλος.
Φέρουμε τα ύψη

και
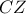
. Ες είναι

ένα τυχαίο σημείο του μικρού τόξου

. Οι ευθείες

και
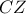
τέμνονται στο

, ενώ οι

και

στο

. Τέλος , αν

το συμμετρικό του

ως προς το

, να αποδείξετε ότι

.
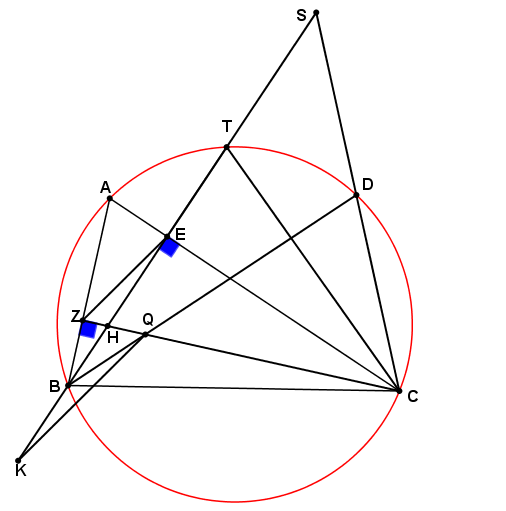
Γεια σου Δημήτρη

Έστω

ορθόκεντρο του

και

.
Είναι

άρα
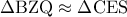
και επίσης

οπότε

.
Είναι γνωστό ότι

οπότε

και έτσι

.
Αντικαθιστώντας στην

έχουμε

και έτσι από το θεώρημα του Θαλή έχουμε το ζητούμενο.
- 329.PNG (32.19 KiB) Προβλήθηκε 768 φορές
Re: Με απλά "μέσα"
Δημοσιεύτηκε: Κυρ Ιουν 28, 2020 4:53 am
από Doloros
ΔΗΜΗΤΡΗΣ ΚΟΛΤΣΗΣ έγραψε: ↑Κυρ Ιουν 28, 2020 12:28 am
Δίνεται οξυγώνιο τρίγωνο

, με

και έστω

ο περιγεγραμμένος του κύκλος.
Φέρουμε τα ύψη

και
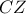
. Ες είναι

ένα τυχαίο σημείο του μικρού τόξου

. Οι ευθείες

και
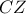
τέμνονται στο

, ενώ οι

και

στο

. Τέλος , αν

το συμμετρικό του

ως προς το

, να αποδείξετε ότι

.
Το τετράπλευρο

είναι εγγράψιμο γιατί οι κορυφές του

βλέπουν υπό ίσες ( και μάλιστα ορθές γωνίες ) τη πλευρά

.
Στο τρίγωνο

η

είναι ταυτόχρονα διάμεσος και ύψος άρα αυτό θα είναι ισοσκελές ,
οπότε η

είναι και διχοτόμος της γωνίας της κορυφής του .
Δηλαδή :

. Αλλά

ως εγγεγραμμένες στο μικρό τόξο της χορδής

.

- με απλά μέσα.png (42.23 KiB) Προβλήθηκε 752 φορές
Έτσι

. Αλλά λόγω του προαναφερθέντος εγγραψίμου τετραπλεύρου

θα είναι :

και η προηγούμενη δίδει:

που μου εξασφαλίζει ότι και το τετράπλευρο

είναι εγγράψιμο.
Από τα εγγράψιμα τώρα τετράπλευρα :

και

έχω ταυτόχρονα:

Re: Με απλά "μέσα"
Δημοσιεύτηκε: Κυρ Ιουν 28, 2020 11:29 am
από Μιχάλης Τσουρακάκης
ΔΗΜΗΤΡΗΣ ΚΟΛΤΣΗΣ έγραψε: ↑Κυρ Ιουν 28, 2020 12:28 am
Δίνεται οξυγώνιο τρίγωνο

, με

και έστω

ο περιγεγραμμένος του κύκλος.
Φέρουμε τα ύψη

και
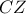
. Ες είναι

ένα τυχαίο σημείο του μικρού τόξου

. Οι ευθείες

και
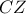
τέμνονται στο

, ενώ οι

και

στο

. Τέλος , αν

το συμμετρικό του

ως προς το

, να αποδείξετε ότι

.
Με

και από την προφανή ισότητα των κόκκινων γωνιών,

είναι εγγράψιμο
Όμως

ως συμπληρώματα των ίσων γωνιών

,επομένως ,

,συνεπώς


- Με απλά μέσα.png (20.5 KiB) Προβλήθηκε 710 φορές
 , με
, με  και έστω
και έστω  ο περιγεγραμμένος του κύκλος.
ο περιγεγραμμένος του κύκλος. και
και 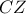 . Ες είναι
. Ες είναι  ένα τυχαίο σημείο του μικρού τόξου
ένα τυχαίο σημείο του μικρού τόξου  . Οι ευθείες
. Οι ευθείες  και
και 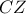 τέμνονται στο
τέμνονται στο  , ενώ οι
, ενώ οι  και
και  στο
στο  . Τέλος , αν
. Τέλος , αν  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  , να αποδείξετε ότι
, να αποδείξετε ότι  .
. , με
, με  και έστω
και έστω  ο περιγεγραμμένος του κύκλος.
ο περιγεγραμμένος του κύκλος. και
και 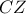 . Ες είναι
. Ες είναι  ένα τυχαίο σημείο του μικρού τόξου
ένα τυχαίο σημείο του μικρού τόξου  . Οι ευθείες
. Οι ευθείες  και
και 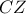 τέμνονται στο
τέμνονται στο  , ενώ οι
, ενώ οι  και
και  στο
στο  . Τέλος , αν
. Τέλος , αν  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  , να αποδείξετε ότι
, να αποδείξετε ότι  .
. ορθόκεντρο του
ορθόκεντρο του  και
και  .
. άρα
άρα 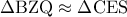 και επίσης
και επίσης  οπότε
οπότε  .
. οπότε
οπότε  και έτσι
και έτσι  .
. έχουμε
έχουμε  και έτσι από το θεώρημα του Θαλή έχουμε το ζητούμενο.
και έτσι από το θεώρημα του Θαλή έχουμε το ζητούμενο.
 είναι εγγράψιμο γιατί οι κορυφές του
είναι εγγράψιμο γιατί οι κορυφές του  βλέπουν υπό ίσες ( και μάλιστα ορθές γωνίες ) τη πλευρά
βλέπουν υπό ίσες ( και μάλιστα ορθές γωνίες ) τη πλευρά  .
. η
η  είναι ταυτόχρονα διάμεσος και ύψος άρα αυτό θα είναι ισοσκελές ,
είναι ταυτόχρονα διάμεσος και ύψος άρα αυτό θα είναι ισοσκελές ,  . Αλλά
. Αλλά  ως εγγεγραμμένες στο μικρό τόξο της χορδής
ως εγγεγραμμένες στο μικρό τόξο της χορδής  .
. . Αλλά λόγω του προαναφερθέντος εγγραψίμου τετραπλεύρου
. Αλλά λόγω του προαναφερθέντος εγγραψίμου τετραπλεύρου  και η προηγούμενη δίδει:
και η προηγούμενη δίδει:  που μου εξασφαλίζει ότι και το τετράπλευρο
που μου εξασφαλίζει ότι και το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.
 και από την προφανή ισότητα των κόκκινων γωνιών,
και από την προφανή ισότητα των κόκκινων γωνιών,  είναι εγγράψιμο
είναι εγγράψιμο ως συμπληρώματα των ίσων γωνιών
ως συμπληρώματα των ίσων γωνιών  ,επομένως ,
,επομένως , ,συνεπώς
,συνεπώς 