Ώρα εφαπτομένης 17

KARKAR · #1

: Ώρα εφαπτομένης 16.png (14.1 KiB) Προβλήθηκε 387 φορές

Στο τετράπλευρο ABCD

του σχήματος , υπολογίστε την $\tan\theta , (\theta=\widehat{CAD})$ .

#2

Βρίσκω το αρμονικό συζυγές

του

ως προς τα $B\,\,\kappa \alpha \iota \,\,D$ . Είναι $\boxed{DF = \frac{{45}}{4}}$ .

Γράφω το ημικύκλιο διαμέτρου $SF = \dfrac{{45}}{4} + 5 = \dfrac{{65}}{4}$ .

Φέρνω τη μεσοκάθετο, ευθεία

του

Αν

το μέσο του

και

το συμμετρικό του

ως προς το

φέρνω στο

κάθετη επί την

και τέμνει το ημικύκλιο στο

.

: Ώρα εφαπτομένης 17_κατασκευή.png (29.35 KiB) Προβλήθηκε 366 φορές

Θα είναι : MS = SL = 4

και άρα $LF = 1 + \dfrac{{45}}{4} = \dfrac{{49}}{4}$ , οπότε

$C{L^2} = SL \cdot LF = 49 \Rightarrow CL = 7$ .

Η

αν προεκταθεί τέμνει τη ευθεία

στο

.

Υπολογισμοί:

$\left\{ \begin{gathered} \tan \omega = \frac{4}{7} \hfill \\ \tan \left( {\omega + \theta } \right) = \frac{{4 + 5}}{7} = \frac{9}{7} \hfill \\ \end{gathered} \right.$ και άρα : $\dfrac{{\tan \omega + \tan \theta }}{{1 - \tan \omega \tan \theta }} = \dfrac{9}{7} \Rightarrow \boxed{\tan \theta = \frac{7}{{17}}}$ .

#3

KARKAR έγραψε: ↑
Τετ Μαρ 11, 2020 10:29 pm
Ώρα εφαπτομένης 16.pngΣτο τετράπλευρο του σχήματος , υπολογίστε την $\tan\theta , (\theta=\widehat{CAD})$ .

Η άσκηση είναι εφαρμογή αυτής

: Εφ-17.png (13.79 KiB) Προβλήθηκε 358 φορές

Σύμφωνα με την παραπομπή, $\displaystyle 4 = \sqrt {\frac{{81 - A{H^2}}}{2}} \Leftrightarrow AH = 7.$ Εύκολα τώρα $\boxed{\tan \theta=\frac{7}{17}}$

Μιχάλης Τσουρακάκης · #4

KARKAR έγραψε: ↑
Τετ Μαρ 11, 2020 10:29 pm
Ώρα εφαπτομένης 16.pngΣτο τετράπλευρο του σχήματος , υπολογίστε την $\tan\theta , (\theta=\widehat{CAD})$ .

Με $AM\bot BD ,DH \bot AC \Rightarrow M,H$ μέσα των $AD,DZ \Rightarrow MH//BC$

Έτσι οι γωνίες $\theta$ είναι ίσες και ABCD

εγγράψιμο $\Rightarrow AS^2=13 . 5=65$ και με Π.Θ στο $\triangle AMS \Rightarrow AM=7$

Από τα όμοια τρίγωνα $AMS,SHD \Rightarrow \dfrac{DH}{7}= \dfrac{5}{AS} = \dfrac{SH}{4} \Rightarrow SH= \dfrac{20}{AS} \Rightarrow AH= \dfrac{AS^2+20 }{AS}= \dfrac{85}{AS}$ και $DH= \dfrac{35}{AS}$

$tan \theta = \dfrac{DH}{AH} = \dfrac{35}{85} = \dfrac{7}{17}$

: Ώρα εφαπτομένης 17.png (38.59 KiB) Προβλήθηκε 315 φορές

p_gianno · #5

: εφαπτ 17B.png (62.61 KiB) Προβλήθηκε 290 φορές

Θεωρώ τον κύκλο (BCD)

και θα δείξω ότι περνά από το σημείο

. Πράγματι αν ο κύκλος δεν περνά από το

αλλά από το σημείο

(της

) τότε θα είναι ZB=ZD

, συνεπώς θα υπάρχουν

σημεία (το

και

) που θα ισαπέχουν από τα άκρα του

που σημαίνει ότι η ευθεία

είναι μεσοκάθετος του

πράγμα άτοπο αφού το σημείο της

δεν ισαπέχει από τα B,D

. Επομένως το

είναι σημείο του κύκλου και το τετράπλευρο ABCD

είναι εγγράψιμο.
Από την ισότητα $AS \cdot SC=BS \cdot SD$ προκύπτει $AS=\sqrt{65}$ ενώ στο τρίγωνο AKS

με Π.Θ υπολογίζουμε AK=7

.
Είναι τώρα $tanx=\frac{4}{7} \,\, (1)$ και $tan(KAD)=tan(x+\theta)=\frac{9}{7} \,\, (2)$ .

Όμως $\displaystyle tan(x+\theta)= \frac{tanx+tan \theta}{1-tanx+tan \theta}$ και με αντικατάσταση των (1)

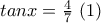και

προκύπτει $\displaystyle tan\theta=\frac{7}{17}$

Ώρα εφαπτομένης 17

Ώρα εφαπτομένης 17

Re: Ώρα εφαπτομένης 17

Re: Ώρα εφαπτομένης 17

Re: Ώρα εφαπτομένης 17

Re: Ώρα εφαπτομένης 17

Μέλη σε σύνδεση