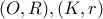 τέμνονται στα σημεία
τέμνονται στα σημεία  . Από τυχόν σημείο
. Από τυχόν σημείο  του
του  φέρω τις
φέρω τις 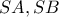 ,
,οι οποίες ξανατέμνουν τον
 στα σημεία
στα σημεία  αντίστοιχα . Δείξτε ότι :
αντίστοιχα . Δείξτε ότι :  .
.Ερώτημα για έρευνα : Αν
 , υπολογίστε το μέγιστο του τμήματος
, υπολογίστε το μέγιστο του τμήματος  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
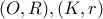 τέμνονται στα σημεία
τέμνονται στα σημεία  . Από τυχόν σημείο
. Από τυχόν σημείο  του
του  φέρω τις
φέρω τις 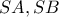 ,
, στα σημεία
στα σημεία  αντίστοιχα . Δείξτε ότι :
αντίστοιχα . Δείξτε ότι :  .
. , υπολογίστε το μέγιστο του τμήματος
, υπολογίστε το μέγιστο του τμήματος  .
.Κάτσε να πάρω εγώ το Όσκαρ
 είναι οι κάθετες από το
είναι οι κάθετες από το  στις χορδές
στις χορδές  του κύκλου
του κύκλου  προφανώς
προφανώς  τα μέσα τους αντίστοιχα και συνεπώς
τα μέσα τους αντίστοιχα και συνεπώς 
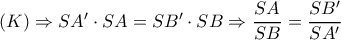

 προκύπτει σύμφωνα με το http://www.cut-the-knot.org/m/Geometry/ ... tras.shtml ότι
προκύπτει σύμφωνα με το http://www.cut-the-knot.org/m/Geometry/ ... tras.shtml ότι 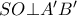 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Βέβαια η απάντηση είναι και άμεση από το γενικευμένο θεώρημα του NagelΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τρί Φεβ 18, 2020 9:41 pmΚάτσε να πάρω εγώ το Όσκαρ
Ανείναι οι κάθετες από το
στις χορδές
του κύκλου
προφανώς
τα μέσα τους αντίστοιχα και συνεπώς

Από το θεώρημα των τεμνόμενων χορδών στον κύκλο
Από τηπροκύπτει σύμφωνα με το http://www.cut-the-knot.org/m/Geometry/ ... tras.shtml ότι
και το ζητούμενο έχει αποδειχθεί.
Την διερεύνηση την αφήνω για άλλον και ας μοιραστώ το όσκαρ
 στο
στο  του κύκλου
του κύκλου  .
.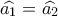 ( Υπό χορδής κι εφαπτομένης)
( Υπό χορδής κι εφαπτομένης) ( εξωτερική εγγεγραμμένου τετράπλευρου)
( εξωτερική εγγεγραμμένου τετράπλευρου) . Τέλος .
. Τέλος . του παλιού σχολικού βιβλίου των Δ. Παπαμιχαήλ -Α. Σκιαδά έκδοση 1986 σελίδα
του παλιού σχολικού βιβλίου των Δ. Παπαμιχαήλ -Α. Σκιαδά έκδοση 1986 σελίδα  .
.Καλημέρα
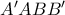 είναι
είναι 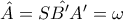

 Αρα το τετράπλευρο
Αρα το τετράπλευρο 

Έχασα το Όσκαρ, αλλά κυνηγάω το Νόμπελ
 Κρατάω το αποτέλεσμα του α) ερωτήματος.
Οι κάθετες από τα
Κρατάω το αποτέλεσμα του α) ερωτήματος.
Οι κάθετες από τα  στις
στις 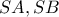 αντίστοιχα τέμνονται στο
αντίστοιχα τέμνονται στο  Φέρνω από το
Φέρνω από το  παράλληλη στην
παράλληλη στην  που τέμνει
που τέμνει  στα
στα 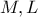 αντίστοιχα. Είναι
αντίστοιχα. Είναι  άρα το
άρα το  είναι μέσο του
είναι μέσο του  κι επειδή το
κι επειδή το  είναι
είναι  το
το  θα είναι το κέντρο αυτού του κύκλου. Από το πρώτο ερώτημα είναι:
θα είναι το κέντρο αυτού του κύκλου. Από το πρώτο ερώτημα είναι: οπότε το
οπότε το  είναι παραλληλόγραμμο. Αλλά,
είναι παραλληλόγραμμο. Αλλά, 

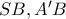 είναι διάμετροι των κύκλων
είναι διάμετροι των κύκλων  αντίστοιχα, οπότε
αντίστοιχα, οπότε  .
. εφαπτόμενο τμήμα στον κύκλο
εφαπτόμενο τμήμα στον κύκλο  και
και  το ύψος του
το ύψος του  . Θέτω
. Θέτω  .
. και
και 

 έχει θετικούς όρους και ο αριθμητής είναι σταθερός , θα γίνεται μέγιστο όταν ο παρανομαστής
έχει θετικούς όρους και ο αριθμητής είναι σταθερός , θα γίνεται μέγιστο όταν ο παρανομαστής  πάρει τη μικρότερη τιμή δηλαδή
πάρει τη μικρότερη τιμή δηλαδή  . Τότε οι
. Τότε οι  γίνονται διάμετροι των δύο κύκλων και
γίνονται διάμετροι των δύο κύκλων και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 19 επισκέπτες