 με τα ύψη του
με τα ύψη του  τις διαμέσους του
τις διαμέσους του  και την διχοτόμο του
και την διχοτόμο του  .
.Αν ισχύουν
 και
και  τότε: Να υπολογιστεί ο λόγος
τότε: Να υπολογιστεί ο λόγος  .
.Το ορθό σχήμα έπεται μέρους της λύσης , συνεπώς θα ..
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 με τα ύψη του
με τα ύψη του  τις διαμέσους του
τις διαμέσους του  και την διχοτόμο του
και την διχοτόμο του  .
. και
και  τότε: Να υπολογιστεί ο λόγος
τότε: Να υπολογιστεί ο λόγος  .
.Καλησπέρα ΓιώργοΓιώργος Μήτσιος έγραψε: ↑Κυρ Ιαν 05, 2020 11:34 amΧαιρετώ. Θεωρούμε τρίγωνομε τα ύψη του
τις διαμέσους του
και την διχοτόμο του
.
Αν ισχύουνκαι
τότε: Να υπολογιστεί ο λόγος
.
Το ορθό σχήμα έπεται μέρους της λύσης , συνεπώς θα .... εμφανιστεί σε επόμενη δημοσίευση! Φιλικά, Γιώργος.
 .
. , έχουμε ότι
, έχουμε ότι  .
. .
. 
 .
. και
και  είναι προφανώς όμοια, οπότε
είναι προφανώς όμοια, οπότε  .
. .
.



 . Τότε, αφού το
. Τότε, αφού το  έχει γωνίες
έχει γωνίες  (από τα 2 προηγούμενα βήματα), έχουμε εύκολα ότι το
(από τα 2 προηγούμενα βήματα), έχουμε εύκολα ότι το  είναι ισόπλευρο.
είναι ισόπλευρο. , άρα
, άρα  , και
, και  .
. .
. είναι από τη λύση του Ορέστη) και σε εύλογο χρονικό διάστημα θα υποβάλω προσωπική προσέγγιση.
Φιλικά, Γιώργος.
είναι από τη λύση του Ορέστη) και σε εύλογο χρονικό διάστημα θα υποβάλω προσωπική προσέγγιση.
Φιλικά, Γιώργος.Ας δούμε μία διαφορετική αντιμετώπιση του Βήματος 1 της προηγούμενης λύσης.Γιώργος Μήτσιος έγραψε: ↑Κυρ Ιαν 05, 2020 11:34 amΧαιρετώ. Θεωρούμε τρίγωνομε τα ύψη του
τις διαμέσους του
και την διχοτόμο του
.
Αν ισχύουνκαι
τότε: Να υπολογιστεί ο λόγος
.
Το ορθό σχήμα έπεται μέρους της λύσης , συνεπώς θα .... εμφανιστεί σε επόμενη δημοσίευση! Φιλικά, Γιώργος.
 , άρα,
, άρα,  , άρα έχουμε
, άρα έχουμε  , οπότε η
, οπότε η  είναι εξωτερική διχοτόμος της
είναι εξωτερική διχοτόμος της  .
. , το
, το  είναι σημείο τομής της εσωτερικής διχοτόμου της
είναι σημείο τομής της εσωτερικής διχοτόμου της  και της εξωτερικής της
και της εξωτερικής της  , οπότε είναι το
, οπότε είναι το  παράκεντρο.
παράκεντρο. είναι εξωτερική διχοτόμος της
είναι εξωτερική διχοτόμος της  , οπότε
, οπότε  .
. Προεκτείνω την
Προεκτείνω την  κατά τμήμα
κατά τμήμα 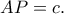 Είναι,
Είναι, 
 άρα το
άρα το  είναι ισόπλευρο και
είναι ισόπλευρο και 

 είναι ισοσκελές τραπέζιο και
είναι ισοσκελές τραπέζιο και  οπότε
οπότε 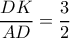

 είναι
είναι  τότε
τότε  και
και 
 μας οδηγεί στην
μας οδηγεί στην  που αντιβαίνει με την δοσμένη , ομοίως και η
που αντιβαίνει με την δοσμένη , ομοίως και η  , άρα απορρίπτονται.
, άρα απορρίπτονται. 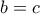 τότε
τότε  συνεπώς έχουμε
συνεπώς έχουμε  αν και μόνον αν
αν και μόνον αν  .
. είναι και ύψος με
είναι και ύψος με 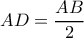 που σημαίνει
που σημαίνει  και
και  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 18 επισκέπτες