 είναι σημείο της πλευράς
είναι σημείο της πλευράς  τετραγώνου
τετραγώνου  τέτοιο ώστε
τέτοιο ώστε  και
και  είναι
είναι το σημείο τομής των
 Να εντοπίσετε σημείο
Να εντοπίσετε σημείο  του τμήματος
του τμήματος  ώστε, αν η
ώστε, αν η  τέμνει τη
τέμνει τη  στο
στο  το
το  να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο
να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι σημείο της πλευράς
είναι σημείο της πλευράς  τετραγώνου
τετραγώνου  τέτοιο ώστε
τέτοιο ώστε  και
και  είναι
είναι  Να εντοπίσετε σημείο
Να εντοπίσετε σημείο  του τμήματος
του τμήματος  ώστε, αν η
ώστε, αν η  τέμνει τη
τέμνει τη  στο
στο  το
το  να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο
να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο 
Καλησπέρα!george visvikis έγραψε: ↑Τρί Ιούλ 09, 2019 7:10 pmΕντοπισμός σημείου και λόγος εμβαδών.pngΤοείναι σημείο της πλευράς
τετραγώνου
τέτοιο ώστε
και
είναι
το σημείο τομής τωνΝα εντοπίσετε σημείο
του τμήματος
ώστε, αν η
τέμνει τη
στο
το
να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο


 αρκεί
αρκεί 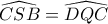 άρα
άρα 
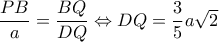 άρα
άρα  .
.
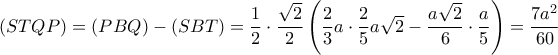
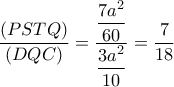
Καλημέρα!1) Έστωgeorge visvikis έγραψε: ↑Τρί Ιούλ 09, 2019 7:10 pmΤοείναι σημείο της πλευράς
τετραγώνου
τέτοιο ώστε
και
είναι
το σημείο τομής τωνΝα εντοπίσετε σημείο
του τμήματος
ώστε, αν η
τέμνει τη
στο
το
να είναι εγγράψιμο. Στη συνέχεια, να υπολογίσετε το λόγο

 το σημείο τομής των διαγωνίων του
το σημείο τομής των διαγωνίων του  . Για να είναι το
. Για να είναι το  εγγράψιμο, αρκεί τα ορθογώνια τρίγωνα
εγγράψιμο, αρκεί τα ορθογώνια τρίγωνα  να είναι όμοια, δηλαδή:
να είναι όμοια, δηλαδή:
 και από τα όμοια
και από τα όμοια 




 τα τρίγωνα
τα τρίγωνα  θα έχουν τις γωνίες στα
θα έχουν τις γωνίες στα 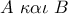 ίσες με
ίσες με 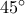 κάθε μια και στα
κάθε μια και στα  ίσες ως παραπληρώματα των
ίσες ως παραπληρώματα των  .
. το σημείο τομής των διαγωνίων του τετραγώνου θα είναι :
το σημείο τομής των διαγωνίων του τετραγώνου θα είναι :  .
. είναι προφανώς όμοια .( Παρόμοια λύση με του Μιχάλη )
είναι προφανώς όμοια .( Παρόμοια λύση με του Μιχάλη )
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 18 επισκέπτες