 είναι τετράγωνο και το
είναι τετράγωνο και το  κανονικό πεντάγωνο. Να βρείτε την οξεία γωνία
κανονικό πεντάγωνο. Να βρείτε την οξεία γωνία  που σχηματίζουν οι
που σχηματίζουν οι 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι τετράγωνο και το
είναι τετράγωνο και το  κανονικό πεντάγωνο. Να βρείτε την οξεία γωνία
κανονικό πεντάγωνο. Να βρείτε την οξεία γωνία  που σχηματίζουν οι
που σχηματίζουν οι 

 και γ) :
και γ) :  .
. , δηλαδή :
, δηλαδή :  .
. , που τελειώνει την άσκηση.
, που τελειώνει την άσκηση. 
 και περιεχόμενη γωνία
και περιεχόμενη γωνία  . Το δεύτερο είναι
. Το δεύτερο είναι  )
) και
και  .Αν
.Αν 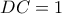 τότε
τότε  .
.
 ( θέτοντας
( θέτοντας  , όπως λέμε..
, όπως λέμε..  είναι
είναι  και με το Π.Θ
και με το Π.Θ  οπότε
οπότε 
 και
και 
 παίρνουμε
παίρνουμε  με
με  άρα
άρα 
 παίρνουμε
παίρνουμε  άρα
άρα  , τότε
, τότε 

 που ισχύει συνεπώς
που ισχύει συνεπώς 
 είναι όμοια οπότε
είναι όμοια οπότε  .
. λοιπόν ανήκει στον περίκυκλο του
λοιπόν ανήκει στον περίκυκλο του  και τελικά
και τελικά  .Φιλικά , Γιώργος.
.Φιλικά , Γιώργος. και
και 

 που ισχύει αφού κάθε γινόμενο ισούται με
που ισχύει αφού κάθε γινόμενο ισούται με 
 είναι εγγράψιμο άρα
είναι εγγράψιμο άρα  κι΄έτσι
κι΄έτσι 

 είναι :
είναι : 
 :
: 
 έχουν κέντρα τα
έχουν κέντρα τα  , αντιστοίχως και το
, αντιστοίχως και το  είναι κοινό τους σημείο.
είναι κοινό τους σημείο.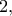 τότε (γνωστό) η διαγώνιος
τότε (γνωστό) η διαγώνιος  . Έτσι
. Έτσι 
 είναι ίσο με το ύψος
είναι ίσο με το ύψος  του τραπεζίου
του τραπεζίου  , για το οποίο από το ορθογώνιο τρίγωνο
, για το οποίο από το ορθογώνιο τρίγωνο  υπολογίζεται ότι ( υπόψη
υπολογίζεται ότι ( υπόψη  ):
):
 είναι ορθογώνιο. Επομένως
είναι ορθογώνιο. Επομένως  και
και
 ανήκει στον περιγεγραμμένο κύκλο του τετραγώνου
ανήκει στον περιγεγραμμένο κύκλο του τετραγώνου  , οπότε
, οπότε 
 συμπίπτει με το
συμπίπτει με το  , δηλαδή ότι είναι το σημείο τομής των τμημάτων
, δηλαδή ότι είναι το σημείο τομής των τμημάτων 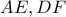 . Αυτό, επειδή
. Αυτό, επειδή  τελειώνει την απόδειξη.
τελειώνει την απόδειξη. , όπως και τα σημεία
, όπως και τα σημεία  είναι συνευθειακά. Αυτά προκύπτουν από τις προφανείς ισότητες:
είναι συνευθειακά. Αυτά προκύπτουν από τις προφανείς ισότητες: και
και 
 τέμνονται στο
τέμνονται στο  Εκ κατασκευής τα κόκκινα τρίγωνα είναι ίσα, καθώς επίσης και τα γαλάζια. Εύκολα βρίσκω:
Εκ κατασκευής τα κόκκινα τρίγωνα είναι ίσα, καθώς επίσης και τα γαλάζια. Εύκολα βρίσκω: 
 και
και 
 τα
τα  είναι ομοκυκλικά και
είναι ομοκυκλικά και 
Όλες ωραίες αλλά αυτή είναι το κάτι άλλο .george visvikis έγραψε: ↑Δευ Ιουν 03, 2019 5:41 pmΕυχαριστώ τον Θανάση, τον Κώστα και το Γιώργο για την ενασχόλησή τους με το θέμα και για τις λύσεις τους. Ας δούμε και μία πιο απλή λύση (δεν είναι δική μου).
Οι κύκλοιτέμνονται στο
Γωνιαίο ζήτημα.ΙΙ.png
Εκ κατασκευής τα κόκκινα τρίγωνα είναι ίσα, καθώς επίσης και τα γαλάζια. Εύκολα βρίσκω:
απ' όπου παίρνωκαι
Άρατα
είναι ομοκυκλικά και

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες