 τριγώνου
τριγώνου  τέμνει τον εγγεγραμμένο κύκλο στα σημεία
τέμνει τον εγγεγραμμένο κύκλο στα σημεία  Οι παράλληλες από τα
Οι παράλληλες από τα  στη
στη 
επανατέμνουν τον κύκλο στα
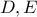 αντίστοιχα. Αν οι
αντίστοιχα. Αν οι  τέμνουν τη
τέμνουν τη  στα
στα  να δείξετε ότι
να δείξετε ότι 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 τριγώνου
τριγώνου  τέμνει τον εγγεγραμμένο κύκλο στα σημεία
τέμνει τον εγγεγραμμένο κύκλο στα σημεία  Οι παράλληλες από τα
Οι παράλληλες από τα  στη
στη 
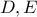 αντίστοιχα. Αν οι
αντίστοιχα. Αν οι  τέμνουν τη
τέμνουν τη  στα
στα  να δείξετε ότι
να δείξετε ότι 
george visvikis έγραψε: ↑Κυρ Φεβ 17, 2019 6:42 pmΊσα τμήματα σε πλευρά.png
Η διάμεσοςτριγώνου
τέμνει τον εγγεγραμμένο κύκλο στα σημεία
Οι παράλληλες από τα
στη
επανατέμνουν τον κύκλο στα
αντίστοιχα. Αν οι
τέμνουν τη
στα
να δείξετε ότι
 Έστω
Έστω  τα σημεία επαφής του έγκυκλου του τριγώνου
τα σημεία επαφής του έγκυκλου του τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα και
αντίστοιχα και  .
.  είναι το σημείο τομής της εκ του
είναι το σημείο τομής της εκ του  παραλλήλου προς την
παραλλήλου προς την  με την
με την  τότε:
τότε:  Με
Με  και
και  το μέσο της
το μέσο της  προκύπτει ότι η δέσμη
προκύπτει ότι η δέσμη  είναι αρμονική οπότε και η σειρά
είναι αρμονική οπότε και η σειρά  είναι αρμονική (όπου
είναι αρμονική (όπου  ).
).
 Το
Το  είναι σημείο της πολικής του
είναι σημείο της πολικής του  , οπότε το
, οπότε το  είναι σημείο της πολικής του
είναι σημείο της πολικής του  , και επίσης από την αρμονική δέσμη
, και επίσης από την αρμονική δέσμη  το
το  είναι σημείο της πολικής του
είναι σημείο της πολικής του  οπότε και το
οπότε και το  είναι σημείο της πολικής του
είναι σημείο της πολικής του  . Άρα
. Άρα  είναι η πολική του
είναι η πολική του  και συνεπώς
και συνεπώς  και με
και με  χορδή του
χορδή του  θα είναι
θα είναι  μεσοκάθετη της
μεσοκάθετη της  άρα και της άλλης βάσης
άρα και της άλλης βάσης  του ισοσκελούς (λόγω εγγραψιμότητας) τραπεζίου , δηλαδή η ευθεία
του ισοσκελούς (λόγω εγγραψιμότητας) τραπεζίου , δηλαδή η ευθεία  είναι άξονας συμμετρίας του
είναι άξονας συμμετρίας του  , οπότε
, οπότε  είναι σημείο και της άλλης διαγωνίου του
είναι σημείο και της άλλης διαγωνίου του  .
. Από την αρμονική δέσμη
Από την αρμονική δέσμη  (αφού
(αφού  η πολική του
η πολική του  ως προς τον
ως προς τον  ) προκύπτει ότι και η δέσμη
) προκύπτει ότι και η δέσμη  είναι αρμονική και με
είναι αρμονική και με  το μέσο της
το μέσο της  από όπου (από την κεντρική δέσμη
από όπου (από την κεντρική δέσμη  με
με  το μέσο και της
το μέσο και της  . Έτσι τα τμήματα
. Έτσι τα τμήματα  έχουν κοινό μέσο (το
έχουν κοινό μέσο (το  ) και συνεπώς
) και συνεπώς  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.  , αρκεί να εφάπτεται στις πλευρές
, αρκεί να εφάπτεται στις πλευρές 
ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τρί Φεβ 19, 2019 10:56 pmgeorge visvikis έγραψε: ↑Κυρ Φεβ 17, 2019 6:42 pmΊσα τμήματα σε πλευρά.png
Η διάμεσοςτριγώνου
τέμνει τον εγγεγραμμένο κύκλο στα σημεία
Οι παράλληλες από τα
στη
επανατέμνουν τον κύκλο στα
αντίστοιχα. Αν οι
τέμνουν τη
στα
να δείξετε ότι
Έστω
τα σημεία επαφής του έγκυκλου του τριγώνου
με τις πλευρές του
αντίστοιχα και
.
Ανείναι το σημείο τομής της εκ του
παραλλήλου προς την
με την
τότε:
Με
και
το μέσο της
προκύπτει ότι η δέσμη
είναι αρμονική οπότε και η σειρά
είναι αρμονική (όπου
).
Ισα τμήματα σε πλευρά.png
Το
είναι σημείο της πολικής του
, οπότε το
είναι σημείο της πολικής του
, και επίσης από την αρμονική δέσμη
το
είναι σημείο της πολικής του
οπότε και το
είναι σημείο της πολικής του
. Άρα
είναι η πολική του
και συνεπώς
και με
χορδή του
θα είναι
μεσοκάθετη της
άρα και της άλλης βάσης
του ισοσκελούς (λόγω εγγραψιμότητας) τραπεζίου , δηλαδή η ευθεία
είναι άξονας συμμετρίας του
, οπότε
είναι σημείο και της άλλης διαγωνίου του
.
Από την αρμονική δέσμη
(αφού
η πολική του
ως προς τον
) προκύπτει ότι και η δέσμη
είναι αρμονική και με
το μέσο της
από όπου (από την κεντρική δέσμη
με
το μέσο και της
. Έτσι τα τμήματα
έχουν κοινό μέσο (το
) και συνεπώς
και το ζητούμενο έχει αποδειχθεί.
Παρατήρηση: Δεν είναι ανάγκη ο κύκλος να είναι ο έγκυκλος του τριγώνου, αρκεί να εφάπτεται στις πλευρές
Υ.Σ. Γιώργο με ενδιαφέρει η πηγή αλλά περισσότερο με ενδιαφέρει η πιθανή λύση που έχεις ή η λύση που έχει η πηγή
Στάθης
Σ' ευχαριστώ Στάθη για τη λύση. Είναι το πρόβλημαΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τρί Φεβ 19, 2019 10:56 pm
Υ.Σ. Γιώργο με ενδιαφέρει η πηγή αλλά περισσότερο με ενδιαφέρει η πιθανή λύση που έχεις ή η λύση που έχει η πηγή
Στάθης
 από IMO Shortlist 2005. Στη σελίδα 16 υπάρχει η επίσημη λύση. (Έχω αλλάξει δύο γράμματα, γιατί δεν μου αρέσει να βάζω σημεία με τα γράμματα
από IMO Shortlist 2005. Στη σελίδα 16 υπάρχει η επίσημη λύση. (Έχω αλλάξει δύο γράμματα, γιατί δεν μου αρέσει να βάζω σημεία με τα γράμματα  ).
). και εφάπτεται στις
και εφάπτεται στις  έστω στα σημεία
έστω στα σημεία 

 ... και τα υπόλοιπα είναι απλά.
... και τα υπόλοιπα είναι απλά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες