george visvikis έγραψε: ↑Δευ Ιαν 14, 2019 11:13 am
Σταθερός λόγος ακτίνων.png
Έστω

μία σταθερή χορδή ενός κύκλου ακτίνας

και ένα μεταβλητό σημείο της

α) Να κατασκευάσετε δύο κύκλους

,

που να εφάπτονται στη χορδή

στο

και εσωτερικά στο έλασσον και αντίστοιχα στο μείζον τόξο
β) Αν

είναι οι ακτίνες αυτών των κύκλων, να δείξετε ότι ο λόγος

είναι σταθερός, ανεξάρτητος της θέσης του

επί της


- statheros_logos_aktinwn.png (38.33 KiB) Προβλήθηκε 1157 φορές
α) Έστω

η μεσοκάθετος της δοσμένης χορδής (

το μέσο της,

ανήκουν στο κύκλο κέντρου

). Έστω

το σημείο τομής της ευθείας
με το κύκλο ακτίνας

και

το σημείο τομής της ακτίνας

με την κάθετη από το σημείο

προς τη δοσμένη χορδή. Κατασκευάζουμε τον κύκλο κέντρου

και ακτίνας

. Ο κύκλος αυτός εφάπτεται του κύκλου ακτίνας

, στο σημείο

.
Έστω

το σημείο τομής της ευθείας

με το κύκλο κέντρου

. Λόγω ομοιoθεσίας θα έχουμε

,

. Άρα θα είναι και
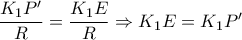
. Στον ίδιο λόγο όμως χωρίζει και το σημείο

την

. Έπομένως τα σημεία

και

ταυτίζονται και ο κύκλος κέντρου

και ακτίνας

είναι ο ζητούμενος. Ομοίως κατασκευάζεται και ο δεύτερος κύκλος.
β) Έστω

το σημείο επαφής του κύκλου κέντρου

με το κύκλο ακτίνας

και

το σημείο τομής των ευθειών

και

. Τότε το σημείο

είναι το ορθόκεντρο του τριγώνου

. Για το ζητούμενο λόγο των ακτινών έχουμε διαδοχικά.

Η τελευταία ισότητα λόγω των ομοίων ορθογώνιων τριγώνων

και

γίνεται

Από το θεώρημα Ceva όμως, ισχύει


 μία σταθερή χορδή ενός κύκλου ακτίνας
μία σταθερή χορδή ενός κύκλου ακτίνας  και ένα μεταβλητό σημείο της
και ένα μεταβλητό σημείο της 
 ,
,  που να εφάπτονται στη χορδή
που να εφάπτονται στη χορδή  στο
στο  και εσωτερικά στο έλασσον και αντίστοιχα στο μείζον τόξο
και εσωτερικά στο έλασσον και αντίστοιχα στο μείζον τόξο 
 είναι οι ακτίνες αυτών των κύκλων, να δείξετε ότι ο λόγος
είναι οι ακτίνες αυτών των κύκλων, να δείξετε ότι ο λόγος  είναι σταθερός, ανεξάρτητος της θέσης του
είναι σταθερός, ανεξάρτητος της θέσης του  επί της
επί της 

 της προέκτασης της
της προέκτασης της 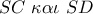 .
. με τις διχοτόμους των
με τις διχοτόμους των  μας δίδουν τα δύο κέντρα
μας δίδουν τα δύο κέντρα  . Όπου
. Όπου  το απόστημα προς τη χορδή
το απόστημα προς τη χορδή  που είναι κάθετη στην δοσμένη χορδή
που είναι κάθετη στην δοσμένη χορδή  .
.  τεμνουν τον κύκλο στα
τεμνουν τον κύκλο στα  αντίστοιχα. Οι
αντίστοιχα. Οι  τέμνουν την κάθετη προς την
τέμνουν την κάθετη προς την 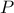 στα
στα  αντίστοιχα
αντίστοιχα  .
.  αφήνει αναλλοίωτους και τους τρεις κύκλους
αφήνει αναλλοίωτους και τους τρεις κύκλους 
 την μετασχηματίζει και κύκλο που διέρχεται από τον πόλο
την μετασχηματίζει και κύκλο που διέρχεται από τον πόλο  που συντρέχουν οι
που συντρέχουν οι  .
.
 )
)  η μεσοκάθετος της δοσμένης χορδής (
η μεσοκάθετος της δοσμένης χορδής ( το μέσο της,
το μέσο της,  ανήκουν στο κύκλο κέντρου
ανήκουν στο κύκλο κέντρου  ). Έστω
). Έστω  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας 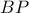 με το κύκλο ακτίνας
με το κύκλο ακτίνας  το σημείο τομής της ακτίνας
το σημείο τομής της ακτίνας  με την κάθετη από το σημείο
με την κάθετη από το σημείο  . Ο κύκλος αυτός εφάπτεται του κύκλου ακτίνας
. Ο κύκλος αυτός εφάπτεται του κύκλου ακτίνας  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας  με το κύκλο κέντρου
με το κύκλο κέντρου  ,
,  . Άρα θα είναι και
. Άρα θα είναι και 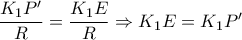 . Στον ίδιο λόγο όμως χωρίζει και το σημείο
. Στον ίδιο λόγο όμως χωρίζει και το σημείο  είναι ο ζητούμενος. Ομοίως κατασκευάζεται και ο δεύτερος κύκλος.
είναι ο ζητούμενος. Ομοίως κατασκευάζεται και ο δεύτερος κύκλος. το σημείο επαφής του κύκλου κέντρου
το σημείο επαφής του κύκλου κέντρου  με το κύκλο ακτίνας
με το κύκλο ακτίνας  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  . Τότε το σημείο
. Τότε το σημείο  . Για το ζητούμενο λόγο των ακτινών έχουμε διαδοχικά.
. Για το ζητούμενο λόγο των ακτινών έχουμε διαδοχικά.
 και
και  γίνεται
γίνεται


 διέρχεται επίσης από το
διέρχεται επίσης από το  . Η ακτίνα
. Η ακτίνα  είναι εκ κατασκευής κάθετη στην
είναι εκ κατασκευής κάθετη στην 
 :
: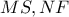 που τέμνονται στο
που τέμνονται στο  . Το
. Το  , άρα το
, άρα το  τέμνει την
τέμνει την  έστω στο
έστω στο  . Ισχύει ότι:
. Ισχύει ότι:  άρα το
άρα το  .
.
 το απόστημα της χορδής
το απόστημα της χορδής  Τότε με Πυθαγόρειο στο
Τότε με Πυθαγόρειο στο  έχουμε:
έχουμε:

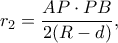 οπότε
οπότε 