
Μία εύκολη κατασκευή του ζητούμενου κύκλου, χωρίς υπολογισμό της ακτίνας του, βασίζεται σε ένα γνωστό
Λήμμα, σύμφωνα με το οποίο η ευθεία

στο σχήμα του Θάνάση, περνάει από το έγκεντρο

του τριγώνου

.
Επομένως, τα σημεία

, προσδιορίζονται ως τα σημεία τομής των

αντιστοίχως, από την δια του σημείου

κάθετη ευθεία επί την διχοτόμο της γωνίας

και άρα, το κέντρο του ζητούμενου κύκλου προκύπτει άμεσα.
Η ως άνω κατασκευή αφορά σε τυχούσες τις ευθείες

και επομένως το πρόβλημα όπως έχει τεθεί, είναι μία είδική περίπτωση.

- Κατασκευή σε κύκλο.
- f 178_t 63593.PNG (18.8 KiB) Προβλήθηκε 743 φορές

Το παραπάνω αναφερόμενο
Λήμμα, οφείλεται στον
Jean-Louis Ayme, εξαίρετο Γάλλο γεωμέτρη και έχει χρησιμοποιηθεί για την απόδειξη του
Θεωρήματος Sawayama - Thebault, από τον ίδιο. (*)
Την απόδειξη αυτού του
Λήμματος, έχουμε δει "μεταγλωτισμένη" παλιότερα,
Εδώ.
Κώστας Βήττας.
(*) Δύο άλλες αποδείξεις του
Θεωρήματος Sawayama - Thebault, βασισμένες στο ίδιο ως άνω δυνατό
Λήμμα, έχουμε δεί
Εδώ.
 παίρνουμε τυχαία κάθετη στην
παίρνουμε τυχαία κάθετη στην  που να την τέμνει εσωτερικά. Να κατασκευαστεί ο ένας από τους 2 κύκλους που εφάπτεται στον ημικύκλιο, στην κάθετη της διαμέτρου και στην διάμετρο ταυτόχρονα. Ένα έξτρα ερώτημα Aν η κάθετη τέμνει την διάμετρο στο
που να την τέμνει εσωτερικά. Να κατασκευαστεί ο ένας από τους 2 κύκλους που εφάπτεται στον ημικύκλιο, στην κάθετη της διαμέτρου και στην διάμετρο ταυτόχρονα. Ένα έξτρα ερώτημα Aν η κάθετη τέμνει την διάμετρο στο  και το κύκλο στο
και το κύκλο στο  τότε μπορεί ο ζητούμενος κύκλος να εφάπτεται στο μέσο της
τότε μπορεί ο ζητούμενος κύκλος να εφάπτεται στο μέσο της 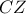 ;
;
 Μία εύκολη κατασκευή του ζητούμενου κύκλου, χωρίς υπολογισμό της ακτίνας του, βασίζεται σε ένα γνωστό Λήμμα, σύμφωνα με το οποίο η ευθεία
Μία εύκολη κατασκευή του ζητούμενου κύκλου, χωρίς υπολογισμό της ακτίνας του, βασίζεται σε ένα γνωστό Λήμμα, σύμφωνα με το οποίο η ευθεία  στο σχήμα του Θάνάση, περνάει από το έγκεντρο
στο σχήμα του Θάνάση, περνάει από το έγκεντρο  του τριγώνου
του τριγώνου  .
. , προσδιορίζονται ως τα σημεία τομής των
, προσδιορίζονται ως τα σημεία τομής των  αντιστοίχως, από την δια του σημείου
αντιστοίχως, από την δια του σημείου  και άρα, το κέντρο του ζητούμενου κύκλου προκύπτει άμεσα.
και άρα, το κέντρο του ζητούμενου κύκλου προκύπτει άμεσα. και επομένως το πρόβλημα όπως έχει τεθεί, είναι μία είδική περίπτωση.
και επομένως το πρόβλημα όπως έχει τεθεί, είναι μία είδική περίπτωση.
 ) : Πρέπει :
) : Πρέπει :  .
. , βρίσκουμε :
, βρίσκουμε :  .
. ο ζητούμενος και
ο ζητούμενος και  το δεδομένο ημικύκλιο. Έστω ακόμα
το δεδομένο ημικύκλιο. Έστω ακόμα  . Ο ομόκεντρος του
. Ο ομόκεντρος του  , διέρχεται κι από το
, διέρχεται κι από το 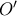 συμμετρικό του
συμμετρικό του  . Εφάπτεται δε
. Εφάπτεται δε  . Το πρώτο πρόβλημα του Απολλώνιου ( Σ(ημείο) ,Σ(ημείο),Ε(υθεία) )
. Το πρώτο πρόβλημα του Απολλώνιου ( Σ(ημείο) ,Σ(ημείο),Ε(υθεία) ) έχουμε την εξίσωση
έχουμε την εξίσωση 

 ή
ή  .
.  .
. τέμνει τη διάμετρο στο
τέμνει τη διάμετρο στο  Το κέντρο
Το κέντρο  του ζητούμενου κύκλου
του ζητούμενου κύκλου  με τη κάθετο από το
με τη κάθετο από το  στη διάμετρο.
στη διάμετρο. ( Δεν είχα τότε ακόμα γραφτεί στο mathematica).
( Δεν είχα τότε ακόμα γραφτεί στο mathematica). είναι τα
είναι τα  και με το ημικύκλιο το
και με το ημικύκλιο το  .
. είναι συνευθειακά αφού
είναι συνευθειακά αφού  και τα
και τα  είναι ισοσκελή.
είναι ισοσκελή.  και δύναμη αντιστροφής
και δύναμη αντιστροφής 

 από το Θ. Ευκλείδη στο
από το Θ. Ευκλείδη στο  από το εγγράψιμο τετράπλευρο
από το εγγράψιμο τετράπλευρο  και η
και η  από τη δύναμη του
από τη δύναμη του 
 με ίδιο πόλο και ίδια δύναμη την μετασχηματίζει στο κύκλο κέντρου
με ίδιο πόλο και ίδια δύναμη την μετασχηματίζει στο κύκλο κέντρου  .
. και οι κύκλοι εφάπτονται.)
και οι κύκλοι εφάπτονται.) , κατασκευάζουμε το τετράγωνο
, κατασκευάζουμε το τετράγωνο  και βρίσκουμε το
και βρίσκουμε το