Έστω το σημείο

και ας είναι

, η προβολή του σημείου

επί της

, αντί του

της εκφώνησης.
Στο τρίγωνο

, με

, έχουμε


, λόγω

και

.
Η ευθεία

τώρα, περνάει από το σημείο έστω

, λόγω του τραπεζίου

και

.

Για να ισχύει το ζητούμενο

, αρκεί να αποδειχθεί ότι η ευθεία

εφάπτεται στον περίκυκλο έστω

του τριγώνου

στο σημείο

.
Αρκεί δηλαδή να αποδειχθεί ότι ισχύει

Από το εγγράψιμο τετράπλευρο

έχουμε

Από

αρκεί να αποδειχθεί ότι ισχύει

Από

, σύμφωνα με το
Θεώρημα Newton, αρκεί να αποδειχθεί ότι η σημειοσειρά
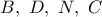
είναι αρμονική, όπου

είναι το συμμετρικό σημείο του

ως προς το

.

- Ίσες γωνίες σε ορθογώνιο τρίγωνο.
- f 178_t 63520.PNG (24.63 KiB) Προβλήθηκε 585 φορές

Στο τρίγωνο

με διατέμνουσα την

, σύμφωνα με το
Θεώρημα Μενελάου,
έχουμε


λόγω

.
Από

και

λόγω

προκύπτει

Από

συμπεραίνεται ότι η σημειοσειρά
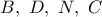
είναι αρμονική.

Γνωστό
Λήμμα στα αρμονικά συζυγή, η απόδειξη του οποίου αφήνεται ως άσκηση στον αναγνώστη

.
Άρα, σύμφωνα με το
Θεώρημα Newton, η

αληθεύει και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας
 το ύψος και
το ύψος και 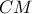 η διάμεσος ορθογωνίου τριγώνου
η διάμεσος ορθογωνίου τριγώνου  με
με  το μέσο του
το μέσο του 
 είναι το σημείο τομής των
είναι το σημείο τομής των  και
και  η προβολή του
η προβολή του  στην
στην  να δείξετε ότι
να δείξετε ότι 
 το ύψος και
το ύψος και 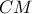 η διάμεσος ορθογωνίου τριγώνου
η διάμεσος ορθογωνίου τριγώνου  με
με  το μέσο του
το μέσο του 
 είναι το σημείο τομής των
είναι το σημείο τομής των  και
και  η προβολή του
η προβολή του  στην
στην  να δείξετε ότι
να δείξετε ότι 
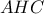 και
και  είναι όμοια και γι αυτό αρκεί να δείξω ότι οι
είναι όμοια και γι αυτό αρκεί να δείξω ότι οι  και
και  είναι κάθετες .
είναι κάθετες . και μοναδιαίο διάνυσμα του κατακόρυφου άξονα το
και μοναδιαίο διάνυσμα του κατακόρυφου άξονα το  , συνεπώς
, συνεπώς  .
. 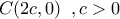 και
και  επειδή
επειδή  και άρα
και άρα 

 . Τώρα
. Τώρα  με συντελεστή διεύθυνσης :
με συντελεστή διεύθυνσης : συνεπώς της καθέτου προς την
συνεπώς της καθέτου προς την  είναι
είναι  .
.
 είναι αντίστοιχα :
είναι αντίστοιχα :
 και ας είναι
και ας είναι  , η προβολή του σημείου
, η προβολή του σημείου  , με
, με  , έχουμε
, έχουμε 
 , λόγω
, λόγω  και
και  .
. τώρα, περνάει από το σημείο έστω
τώρα, περνάει από το σημείο έστω  , λόγω του τραπεζίου
, λόγω του τραπεζίου  και
και  .
. Για να ισχύει το ζητούμενο
Για να ισχύει το ζητούμενο  , αρκεί να αποδειχθεί ότι η ευθεία
, αρκεί να αποδειχθεί ότι η ευθεία  εφάπτεται στον περίκυκλο έστω
εφάπτεται στον περίκυκλο έστω  του τριγώνου
του τριγώνου  στο σημείο
στο σημείο  .
.
 έχουμε
έχουμε 
 αρκεί να αποδειχθεί ότι ισχύει
αρκεί να αποδειχθεί ότι ισχύει 
 , σύμφωνα με το
, σύμφωνα με το 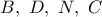 είναι αρμονική, όπου
είναι αρμονική, όπου  είναι το συμμετρικό σημείο του
είναι το συμμετρικό σημείο του  .
.
 με διατέμνουσα την
με διατέμνουσα την  , σύμφωνα με το
, σύμφωνα με το 
 λόγω
λόγω  .
. και
και  λόγω
λόγω  προκύπτει
προκύπτει 
 συμπεραίνεται ότι η σημειοσειρά
συμπεραίνεται ότι η σημειοσειρά  Γνωστό
Γνωστό  .
.