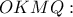Δίδεται ημικύκλιο διαμέτρου
 και σταθερό σημείο
και σταθερό σημείο  της διαμέτρου (πιο κοντά στο
της διαμέτρου (πιο κοντά στο  ). Έστω η κάθετη ευθεία
). Έστω η κάθετη ευθεία  στην
στην  στο
στο  .
.Να φέρετε εφαπτόμενο τμήμα του ημικυκλίου που να τέμνει την ημιευθεία
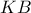 στο
στο  και την ευθεία
και την ευθεία  στο
στο  , ώστε το σημείο επαφής
, ώστε το σημείο επαφής  να είναι μέσο του
να είναι μέσο του  .
.
 ,τότε
,τότε 

 με τέμνουσα
με τέμνουσα 
 του κέντρο του ημικυκλίου και
του κέντρο του ημικυκλίου και