 , τριγώνου
, τριγώνου  , κατά τμήμα
, κατά τμήμα  . Οι ημιευθείες
. Οι ημιευθείες  τέμνουν τις προεκτάσεις των
τέμνουν τις προεκτάσεις των  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα.α) Υπολογίστε το λόγο :
 ... β) Υπολογίστε το λόγο :
... β) Υπολογίστε το λόγο : 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , τριγώνου
, τριγώνου  , κατά τμήμα
, κατά τμήμα  . Οι ημιευθείες
. Οι ημιευθείες  τέμνουν τις προεκτάσεις των
τέμνουν τις προεκτάσεις των  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα. ... β) Υπολογίστε το λόγο :
... β) Υπολογίστε το λόγο : 
Καλημέρα Θανάση και Χρόνια Πολλά σε όλους!
 με διατέμνουσα
με διατέμνουσα  , και προκύπτει (χρησιμοποιούμε ότι
, και προκύπτει (χρησιμοποιούμε ότι  )
)  (1).
(1). με διατέμνουσα
με διατέμνουσα  και προκύπτει (χρησιμοποιούμε ότι
και προκύπτει (χρησιμοποιούμε ότι  ) ότι
) ότι  (2).
(2). και οι (1), (2) γίνονται
και οι (1), (2) γίνονται  (3) και
(3) και  (4).
(4). και οι (3), (4) γίνονται
και οι (3), (4) γίνονται 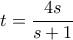 και
και  .
. .
. και
και  .
. και
και  .
. (αφού
(αφού  ) και άρα τα τρίγωνα
) και άρα τα τρίγωνα  είναι όμοια, οπότε
είναι όμοια, οπότε  .
. )
)  (αφού
(αφού  από το (α) ερώτημα)
από το (α) ερώτημα) .
.ΧΡΟΝΙΑ ΠΟΛΛΑ
 φέρνω παράλληλη στη
φέρνω παράλληλη στη  που τέμνει τις
που τέμνει τις  στα
στα  και κάθετη στη
και κάθετη στη  που τέμνει τις
που τέμνει τις  στα
στα  αντίστοιχα.
α)
αντίστοιχα.
α) 

 Αλλά, είναι γνωστό ότι
Αλλά, είναι γνωστό ότι


 της διαμέσου λόγω του Θ.
της διαμέσου λόγω του Θ.  θα είναι
θα είναι 
 το σημείο τομής της
το σημείο τομής της  με τη
με τη  . Θέτω
. Θέτω  και
και  . Θα είναι, λόγω κεντρικής δέσμης, το
. Θα είναι, λόγω κεντρικής δέσμης, το  μέσο του
μέσο του  και η τετράδα
και η τετράδα  αρμονική οπότε:
αρμονική οπότε:  ,
, 
 .
.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες