 το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  Ο
Ο 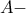 παρεγγεγραμμένος κύκλος
παρεγγεγραμμένος κύκλος  εφάπτεται της
εφάπτεται της  στο
στο 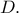
Η
 επανατέμνει τον
επανατέμνει τον  στο
στο 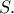 να δείξετε ότι η
να δείξετε ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  Ο
Ο 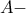 παρεγγεγραμμένος κύκλος
παρεγγεγραμμένος κύκλος  εφάπτεται της
εφάπτεται της  στο
στο 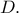
 επανατέμνει τον
επανατέμνει τον  στο
στο 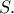 να δείξετε ότι η
να δείξετε ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία 
 το μέσο του
το μέσο του  . Έστω ακόμη
. Έστω ακόμη  το σημείο που ο εγγεγραμμένος κύκλος εφάπτεται στην
το σημείο που ο εγγεγραμμένος κύκλος εφάπτεται στην  δηλαδή το σημείο της
δηλαδή το σημείο της  ώστε
ώστε  . Αφού
. Αφού  μέσο της υποτείνουσας έχουμε ότι
μέσο της υποτείνουσας έχουμε ότι  . Όμως ταυτόχρονα ισχύει ότι
. Όμως ταυτόχρονα ισχύει ότι 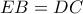 , άρα εύκολα προκύπτει ότι
, άρα εύκολα προκύπτει ότι  .
. 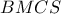 είναι εγγράψιμο, οπότε θα προκύπτει η ζητούμενη διχοτόμηση.
είναι εγγράψιμο, οπότε θα προκύπτει η ζητούμενη διχοτόμηση. .
. το μέσο του
το μέσο του  . Η παραπάνω σχέση γίνεται
. Η παραπάνω σχέση γίνεται 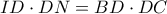 .
. να είναι εγγράψιμο. Ως γνωστό το
να είναι εγγράψιμο. Ως γνωστό το  είναι εγγράψιμο, όπου
είναι εγγράψιμο, όπου  το παράκεντρο της κορυφής
το παράκεντρο της κορυφής  , και ακόμη έχουμε
, και ακόμη έχουμε  , αφού
, αφού  μέσο του
μέσο του  , δηλαδή
, δηλαδή 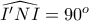 . Όμως είναι
. Όμως είναι 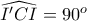 , οπότε έχουμε ότι το
, οπότε έχουμε ότι το 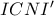 είναι εγγράψιμο, άρα τελικά προκύπτει ότι το
είναι εγγράψιμο, άρα τελικά προκύπτει ότι το  είναι εγγράψιμο!
είναι εγγράψιμο! ,
,  τα σημεία τομής των
τα σημεία τομής των  ,
,  με τον παραγεγραμμένο κύκλο.
με τον παραγεγραμμένο κύκλο. φέρω κάθετη στην
φέρω κάθετη στην  και από το
και από το  φέρω κάθετη στην
φέρω κάθετη στην  .
. τότε οι κόκκινες γωνίες
τότε οι κόκκινες γωνίες  και
και 
 είναι σημείο του παραγεγραμμένου κύκλου.
είναι σημείο του παραγεγραμμένου κύκλου.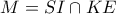 ,
,  τότε το
τότε το  είναι προφανώς περιγεγραμμένο (
είναι προφανώς περιγεγραμμένο ( ).
). , αλλά και
, αλλά και 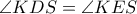 , οπότε
, οπότε  .
. είναι ισοσκελές και θα είναι
είναι ισοσκελές και θα είναι  υψος και διχοτόμος.
υψος και διχοτόμος.
 Έστω
Έστω  , το σημείο επαφής του εγγεγραμμένου κύκλου
, το σημείο επαφής του εγγεγραμμένου κύκλου  στην πλευρά
στην πλευρά  και ας είναι
και ας είναι  , το αντιδιαμετρικό σημείο του
, το αντιδιαμετρικό σημείο του  .
. είναι συνευθειακά ( γνωστό αποτέλεσμα ) και έστω
είναι συνευθειακά ( γνωστό αποτέλεσμα ) και έστω  , τα σημεία επαφής του
, τα σημεία επαφής του 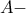 παρεγγεγραμμένου κύκλου, στις ευθείες των πλευρών
παρεγγεγραμμένου κύκλου, στις ευθείες των πλευρών  , αντιστοίχως.
, αντιστοίχως. και
και 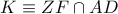 .
. Η ευθεία
Η ευθεία  ταυτίζεται με την Πολική ευθεία του σημείου
ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο 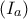 και επειδή περνάει από το σημείο
και επειδή περνάει από το σημείο  , έχουμε το ότι η ευθεία
, έχουμε το ότι η ευθεία  ταυτίζεται με την Πολική ευθεία του σημείου
ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον ίδιο κύκλο, γιατί συνδέει το σημείο
ως προς τον ίδιο κύκλο, γιατί συνδέει το σημείο  με το σημείο
με το σημείο  , επαφής της εφαπτομένης του κύκλου
, επαφής της εφαπτομένης του κύκλου 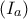 από το σημείο
από το σημείο  .
. είναι αρμονική και ισχύει
είναι αρμονική και ισχύει  .
. τώρα, είναι αρμονική και τεμνόμενη από την ευθεία
τώρα, είναι αρμονική και τεμνόμενη από την ευθεία  μας δίνει την αρμονική σημειοσειρά
μας δίνει την αρμονική σημειοσειρά  .
.
 Ορίζουμε το σημείο
Ορίζουμε το σημείο  της εκφώνησης, ως την προβολή του σημείου
της εκφώνησης, ως την προβολή του σημείου  επί της ευθείας
επί της ευθείας  και λόγω της αρμονικής δέσμης
και λόγω της αρμονικής δέσμης  με
με  , προκύπτει ότι η ευθεία
, προκύπτει ότι η ευθεία  διχοτομεί την γωνία
διχοτομεί την γωνία 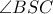 και αρκεί ως ισοδύναμο ζητούμενο, να αποδειχθεί το σημείο
και αρκεί ως ισοδύναμο ζητούμενο, να αποδειχθεί το σημείο  όπως ορίστηκε, ανήκει στον κύκλο
όπως ορίστηκε, ανήκει στον κύκλο 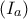 .
. , κατά προέκταση της ευθείας
, κατά προέκταση της ευθείας  προς το μέρος του
προς το μέρος του  και έχουμε ότι η δέσμη
και έχουμε ότι η δέσμη  είναι αρμονική, λόγω
είναι αρμονική, λόγω 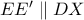 και
και  .
. φέρνουμε την ημιευθεία
φέρνουμε την ημιευθεία  κάθετη επί την
κάθετη επί την  προς το μέρος που δεν κείται το
προς το μέρος που δεν κείται το  .
. τώρα, σχηματίζουν ίσες γωνίες
τώρα, σχηματίζουν ίσες γωνίες  από
από  και
και  και
και 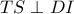 και
και 
 και επομένως, οι δέσμες αυτές έχουν ίσους Διπλούς λόγους και άρα, η δέσμη
και επομένως, οι δέσμες αυτές έχουν ίσους Διπλούς λόγους και άρα, η δέσμη  είναι αρμονική.
είναι αρμονική. και επομένως, ισχύει
και επομένως, ισχύει  όπου
όπου  .
. προκύπτει ότι το σημείο
προκύπτει ότι το σημείο  ταυτίζεται με το αντιδιαμετρικό σημείο του
ταυτίζεται με το αντιδιαμετρικό σημείο του  και άρα, το σημείο
και άρα, το σημείο  ανήκει στον κύκλο
ανήκει στον κύκλο  λόγω
λόγω 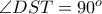 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. ανήκει στον παράκεντρο. Μέχρι τώρα δεν βρήκα
ανήκει στον παράκεντρο. Μέχρι τώρα δεν βρήκα και άξονα
και άξονα  (καφέ άξονες)
(καφέ άξονες) και προσδιορίζω τις συντεταγμένες του
και προσδιορίζω τις συντεταγμένες του λύνοντας το ακόλουθο σύστημα (παράκεντρου κύκλου, ευθείας
λύνοντας το ακόλουθο σύστημα (παράκεντρου κύκλου, ευθείας  )
)

 . (Παράλληλο με το πρώτο, κόκκινοι άξονες).
. (Παράλληλο με το πρώτο, κόκκινοι άξονες). ,
,  ,
,  σε αυτό το σύστημα είναι
σε αυτό το σύστημα είναι  ,
,
 , ενώ οι συντελεστές διεύθυνσης των ευθειών
, ενώ οι συντελεστές διεύθυνσης των ευθειών ,
, 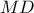 ,
,  θα είναι
θα είναι
 ,
,  δίνεται από τον τύπο
δίνεται από τον τύπο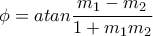

 είναι ομοκυκλικά, τότε για να αποδείξω την τελευταία σχέση
είναι ομοκυκλικά, τότε για να αποδείξω την τελευταία σχέση
 και
και 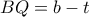 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες