 κινείται στο τεταρτοκύκλιο
κινείται στο τεταρτοκύκλιο  , ακτίνας
, ακτίνας  . Με διάμετρο την
. Με διάμετρο την 
γράφουμε ημικύκλιο , το οποίο τέμνει την
 στο
στο  και έχει μέσο το
και έχει μέσο το  .
.Υπολογίστε το μέγιστο του τμήματος
 .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 κινείται στο τεταρτοκύκλιο
κινείται στο τεταρτοκύκλιο  , ακτίνας
, ακτίνας  . Με διάμετρο την
. Με διάμετρο την 
 στο
στο  και έχει μέσο το
και έχει μέσο το  .
. .
.Στάθης
Αν
 τότε
τότε  και άρα η χορδή
και άρα η χορδή  είναι
είναι  . Tώρα, στον μικρό κύκλο η
. Tώρα, στον μικρό κύκλο η  είναι διάμετρος άρα η χορδή του
είναι διάμετρος άρα η χορδή του 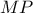 , την οποία βλέπει εγγεγραμμένη
, την οποία βλέπει εγγεγραμμένη  , είναι
, είναι  .
.  , το οποίο λαμβάνεται για
, το οποίο λαμβάνεται για 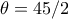 (δεκτό).
(δεκτό).Ας δούμε και μια αμιγώς γεωμετρική λύση
 το σημείο τομής του ημικυκλίου με την
το σημείο τομής του ημικυκλίου με την  . Τότε είναι
. Τότε είναι 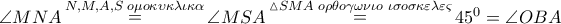

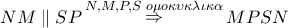 ισοσκελές τραπέζιο , άρα
ισοσκελές τραπέζιο , άρα  με μέγιστη τιμή (αφού
με μέγιστη τιμή (αφού  (λόγω του ημικυκλίου)) όταν το
(λόγω του ημικυκλίου)) όταν το  πάρει τη θέση του μέσου του τεταρτοκυκλίου , οπότε
πάρει τη θέση του μέσου του τεταρτοκυκλίου , οπότε  συνευθειακά.
συνευθειακά. 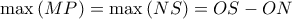
 και το ζητούμενο έχει υπολογιστεί.
και το ζητούμενο έχει υπολογιστεί.Θα χρησιμοποιήσω το παρακάτω λήμμα:
 σημείο ημικυκλίου διαμέτρου
σημείο ημικυκλίου διαμέτρου  και
και  το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  Τότε το
Τότε το  μεγιστοποιείται
μεγιστοποιείται  είναι ισοσκελές και παίρνει μέγιστη τιμή
είναι ισοσκελές και παίρνει μέγιστη τιμή 
 η ακτίνα του τεταρτοκυκλίου. Προφανώς το
η ακτίνα του τεταρτοκυκλίου. Προφανώς το  είναι το έγκεντρο του ορθογωνίου τριγώνου
είναι το έγκεντρο του ορθογωνίου τριγώνου  που έχει
που έχει  και σύμφωνα με το παραπάνω λήμμα θα είναι
και σύμφωνα με το παραπάνω λήμμα θα είναι  και αυτό συμβαίνει
και αυτό συμβαίνει  είναι ισοσκελές, δηλαδή το
είναι ισοσκελές, δηλαδή το  είναι το μέσο του τεταρτοκυκλίου.
είναι το μέσο του τεταρτοκυκλίου. το σημείο τομής της
το σημείο τομής της  με το ημικύκλιο.
με το ημικύκλιο. 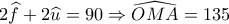 . Επομένως το
. Επομένως το  κινείται σε ημικύκλιο διαμέτρου
κινείται σε ημικύκλιο διαμέτρου  και το
και το  στο τόξο
στο τόξο  που αντιστοιχεί σε εγγεγραμμένη
που αντιστοιχεί σε εγγεγραμμένη  δηλ. επίκεντρη
δηλ. επίκεντρη  . Αρα η
. Αρα η  διέρχεται πάντοτε από το σημείο
διέρχεται πάντοτε από το σημείο  που είναι η τομή του κύκλου διαμέτρου
που είναι η τομή του κύκλου διαμέτρου  με την μεσοκάθετη του
με την μεσοκάθετη του  . Προφανώς όταν
. Προφανώς όταν  κάθετη στην
κάθετη στην  έχουμε το
έχουμε το 
 (dotted line).
(dotted line). σημείο ημικυκλίου διαμέτρου
σημείο ημικυκλίου διαμέτρου  και
και  το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  Τότε το
Τότε το  μεγιστοποιείται
μεγιστοποιείται  είναι ισοσκελές και παίρνει μέγιστη τιμή
είναι ισοσκελές και παίρνει μέγιστη τιμή 
 η διάμετρος που είναι κάθετη στη
η διάμετρος που είναι κάθετη στη  και
και  το έγκεντρο του
το έγκεντρο του  Επειδή
Επειδή  ο γεωμετρικός τόπος του
ο γεωμετρικός τόπος του  είναι το κόκκινο τόξο που φαίνεται στο σχήμα. Αυτό όμως το τόξο ανήκει
είναι το κόκκινο τόξο που φαίνεται στο σχήμα. Αυτό όμως το τόξο ανήκει  άρα
άρα  Αλλά,
Αλλά, 

 η πλευρά
η πλευρά  και η γωνία
και η γωνία  είναι σταθερές,
είναι σταθερές,  μεγιστοποιείται στο ισοσκελές τρίγωνο. Για την γενίκευση είναι:
μεγιστοποιείται στο ισοσκελές τρίγωνο. Για την γενίκευση είναι:  όπου
όπου 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες