Σελίδα 1 από 1
Άλλος λόγος
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 9:14 pm
από KARKAR

- Άλλος λόγος.png (20.58 KiB) Προβλήθηκε 554 φορές
Δύο κύκλοι

και

, με

, τέμνονται στα σημεία

.
Σημείο

κινείται στον

"ανατολικότερα" της κοινής χορδής , ώστε η

να τέμνει τον

σε σημείο

. Δείξτε ότι ο λόγος

παραμένει σταθερός .
Re: Άλλος λόγος
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:48 pm
από Mihalis_Lambrou
KARKAR έγραψε: ↑Δευ Ιουν 11, 2018 9:14 pm
Δύο κύκλοι

και

, με

, τέμνονται στα σημεία

.
Σημείο

κινείται στον

"ανατολικότερα" της κοινής χορδής , ώστε η

να τέμνει τον

σε σημείο

. Δείξτε ότι ο λόγος

παραμένει σταθερός .
Από τον Νόμο των ημιτόνων

Όμως οι γωνίες

είναι σταθερές καθώς

και η τελευταία βαίνει στο σταθερό (μείζον) τόξο

του μικρού κύκλου.
Επίσης με χρήση της

σταθερό (βαίνει στο (μικρό) τόξο

του μεγάλου κύκλου) είναι

ίσον διαφορά σταθερών.
Re: Άλλος λόγος
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 12:16 am
από Doloros
Αν η

στην προέκτασή της προς το

τέμνει τον

στο

θα είναι :

αφού

, έτσι θα έχουμε ταυτόχρονα:

- Αλλος λόγος_νέος_Karkar.png (22.93 KiB) Προβλήθηκε 529 φορές
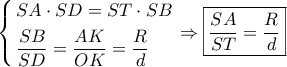
Re: Άλλος λόγος
Δημοσιεύτηκε: Τρί Ιουν 12, 2018 12:34 am
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Δευ Ιουν 11, 2018 9:14 pm
Άλλος λόγος.png Δύο κύκλοι

και

, με

, τέμνονται στα σημεία

.
Σημείο

κινείται στον

"ανατολικότερα" της κοινής χορδής , ώστε η

να τέμνει τον

σε σημείο

. Δείξτε ότι ο λόγος

παραμένει σταθερός .
Λόγω συμμετρίας των

ως προς την

και σχέσης επίκεντρης –εγγεγραμμένης , οι μπλε γωνίες είναι ίσες όπως και οι πράσινες
Έτσι ,


- a.l.png (26.22 KiB) Προβλήθηκε 526 φορές
 και
και  , με
, με  , τέμνονται στα σημεία
, τέμνονται στα σημεία  .
. κινείται στον
κινείται στον  "ανατολικότερα" της κοινής χορδής , ώστε η
"ανατολικότερα" της κοινής χορδής , ώστε η 
 σε σημείο
σε σημείο  . Δείξτε ότι ο λόγος
. Δείξτε ότι ο λόγος  παραμένει σταθερός .
παραμένει σταθερός . και
και  , με
, με  , τέμνονται στα σημεία
, τέμνονται στα σημεία  .
. κινείται στον
κινείται στον  "ανατολικότερα" της κοινής χορδής , ώστε η
"ανατολικότερα" της κοινής χορδής , ώστε η 
 σε σημείο
σε σημείο  . Δείξτε ότι ο λόγος
. Δείξτε ότι ο λόγος  παραμένει σταθερός .
παραμένει σταθερός .
 είναι σταθερές καθώς
είναι σταθερές καθώς  και η τελευταία βαίνει στο σταθερό (μείζον) τόξο
και η τελευταία βαίνει στο σταθερό (μείζον) τόξο  του μικρού κύκλου.
του μικρού κύκλου.  σταθερό (βαίνει στο (μικρό) τόξο
σταθερό (βαίνει στο (μικρό) τόξο  ίσον διαφορά σταθερών.
ίσον διαφορά σταθερών. στην προέκτασή της προς το
στην προέκτασή της προς το  τέμνει τον
τέμνει τον  θα είναι :
θα είναι :  αφού
αφού  , έτσι θα έχουμε ταυτόχρονα:
, έτσι θα έχουμε ταυτόχρονα: 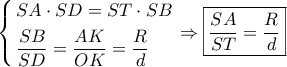
 ως προς την
ως προς την  και σχέσης επίκεντρης –εγγεγραμμένης , οι μπλε γωνίες είναι ίσες όπως και οι πράσινες
και σχέσης επίκεντρης –εγγεγραμμένης , οι μπλε γωνίες είναι ίσες όπως και οι πράσινες