 με
με  ο εγγεγραμμένος του κύκλος έχει
ο εγγεγραμμένος του κύκλος έχει κέντρο το
 και εφάπτεται των
και εφάπτεται των  στα
στα  αντίστοιχα.
αντίστοιχα.Έστω ακόμα
 το βαρύκεντρο του
το βαρύκεντρο του  . Οι
. Οι  τέμνονται στο
τέμνονται στο  , ενώ
, ενώ Η ευθεία
 τέμνει την
τέμνει την 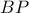 στο
στο  . Δείξετε ότι
. Δείξετε ότι  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 με
με  ο εγγεγραμμένος του κύκλος έχει
ο εγγεγραμμένος του κύκλος έχει  και εφάπτεται των
και εφάπτεται των  στα
στα  αντίστοιχα.
αντίστοιχα. το βαρύκεντρο του
το βαρύκεντρο του  . Οι
. Οι  τέμνονται στο
τέμνονται στο  , ενώ
, ενώ  τέμνει την
τέμνει την 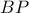 στο
στο  . Δείξετε ότι
. Δείξετε ότι  .
. τέμνει την
τέμνει την  στο
στο  .
. .
. .
.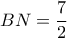 .
.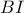 διχοτομεί την
διχοτομεί την  , άρα από Θ. Διχοτόμων,
, άρα από Θ. Διχοτόμων,  .
.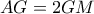 .
. .
. .
. (φαίνονται στο σχήμα).
(φαίνονται στο σχήμα). με διατέμνουσα την
με διατέμνουσα την  , προκύπτει
, προκύπτει  .
. με διατέμνουσα την
με διατέμνουσα την 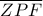 , προκύπτει
, προκύπτει  .
. , άρα
, άρα  , και
, και 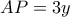 . Έτσι,
. Έτσι,  .
. .
. .
. .
. , το
, το  είναι παραλληλόγραμμο, έτσι
είναι παραλληλόγραμμο, έτσι  .
.Από το Θ.διχοτόμων στο τρίγωνο
 είναι:
είναι:  και στο τρίγωνο
και στο τρίγωνο  :
:  .
.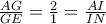 οπότε
οπότε 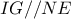 . Ακόμη
. Ακόμη  άρα
άρα  .
.  , έτσι
, έτσι  με συνέπεια το
με συνέπεια το  μέσο του
μέσο του  και το
και το  μέσο του
μέσο του  .
.  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες