Σελίδα 1 από 1
Re: Υπολογισμός γωνίας σε τετράπλευρο.
Δημοσιεύτηκε: Σάβ Απρ 28, 2018 12:31 am
από Doloros

- Υπολογισμός γωνίας σε τετράπλευρο.png (36.65 KiB) Προβλήθηκε 528 φορές
Αύριο τα λόγια .
Edit: ¨άρση απόκρυψης
Re: Υπολογισμός γωνίας σε τετράπλευρο.
Δημοσιεύτηκε: Σάβ Απρ 28, 2018 1:40 am
από Μιχάλης Τσουρακάκης
Φανης Θεοφανιδης έγραψε: ↑Παρ Απρ 27, 2018 10:30 pm
2.png
Καλησπέρα.
Στο τετράπλευρο 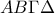 του παραπάνω σχήματος, ισχύει ότι:
του παραπάνω σχήματος, ισχύει ότι:  .
.
Υπολογίστε το μέτρο της γωνίας  .
.
Έστω

το κέντρο του περίκυκλου του

και

η ακτίνα του
Από τη σχέση επίκεντρης- εγγεγραμμένης θα έχουμε

και

Τα τρίγωνα

είναι ίσα αφού έχουν
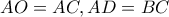
και

άρα

Επομένως η

σχηματίζει με τις

ίσες γωνίες

άρα

συνευθειακά και


- γωνία.png (12.43 KiB) Προβλήθηκε 520 φορές
Re: Υπολογισμός γωνίας σε τετράπλευρο.
Δημοσιεύτηκε: Σάβ Απρ 28, 2018 11:20 am
από Doloros
Γράφω το κύκλο

που τέμνει την ευθεία

ακόμα στο

. Αβίαστα προκύπτει ότι

και συνεπώς αν φέρουμε τη κάθετη από το

- Υπολογισμός γωνίας σε τετράπλευρο_ok.png (40.84 KiB) Προβλήθηκε 488 φορές

στην

η προκύπτουσα χορδή

είναι μεσοκάθετη στην ακτίνα

. Αναγκαστικά τώρα : το τρίγωνο
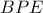
είναι ισόπλευρο και άρα :

, op;ote το μεν τετράπλευρο

είναι παραλληλόγραμμο , ενώ το τετράπλευρο

είναι ισοσκελές τραπέζιο
και έτσι

Re: Υπολογισμός γωνίας σε τετράπλευρο.
Δημοσιεύτηκε: Σάβ Απρ 28, 2018 3:08 pm
από Ορέστης Λιγνός
Θα αποδείξουμε το ισοδύναμο πρόβλημα:
Αν τετράπλευρο

έχει

και

, τότε

.
Απόδειξη
Φέρνουμε την

, και έστω ότι τέμνει την εκ του

παραλλήλου προς την

, στο σημείο

.
Τότε, από το ορθογώνιο
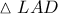
, είναι

, και χρησιμοποιώντας την παραλληλία

, προκύπτουν οι γωνίες του σχήματος.
Τότε,

εγγράψιμο. Επίσης,

τραπέζιο, και άρα το

είναι ισοσκελές τραπέζιο.
Έτσι,

(1).
Αφού όμως

(2).
Επίσης, το
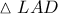
είναι ορθογώνιο, με

, άρα

(3).
Από (1), (2), (3) είναι

, άρα

, ό.έ.δ.

- GONIA-FANIS.ggb.png (29.25 KiB) Προβλήθηκε 471 φορές
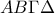 του παραπάνω σχήματος, ισχύει ότι:
του παραπάνω σχήματος, ισχύει ότι:  .
. .
.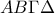 του παραπάνω σχήματος, ισχύει ότι:
του παραπάνω σχήματος, ισχύει ότι:  .
. .
. το κέντρο του περίκυκλου του
το κέντρο του περίκυκλου του  και
και  η ακτίνα του
η ακτίνα του και
και 
 είναι ίσα αφού έχουν
είναι ίσα αφού έχουν 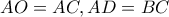
 άρα
άρα 
 σχηματίζει με τις
σχηματίζει με τις  ίσες γωνίες
ίσες γωνίες 
 συνευθειακά και
συνευθειακά και 
 που τέμνει την ευθεία
που τέμνει την ευθεία  ακόμα στο
ακόμα στο  . Αβίαστα προκύπτει ότι
. Αβίαστα προκύπτει ότι  και συνεπώς αν φέρουμε τη κάθετη από το
και συνεπώς αν φέρουμε τη κάθετη από το  στην
στην  η προκύπτουσα χορδή
η προκύπτουσα χορδή  είναι μεσοκάθετη στην ακτίνα
είναι μεσοκάθετη στην ακτίνα  . Αναγκαστικά τώρα : το τρίγωνο
. Αναγκαστικά τώρα : το τρίγωνο 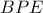 είναι ισόπλευρο και άρα :
είναι ισόπλευρο και άρα :  , op;ote το μεν τετράπλευρο
, op;ote το μεν τετράπλευρο  είναι παραλληλόγραμμο , ενώ το τετράπλευρο
είναι παραλληλόγραμμο , ενώ το τετράπλευρο  είναι ισοσκελές τραπέζιο
είναι ισοσκελές τραπέζιο 
 έχει
έχει  και
και  , τότε
, τότε  .
. , και έστω ότι τέμνει την εκ του
, και έστω ότι τέμνει την εκ του  παραλλήλου προς την
παραλλήλου προς την  , στο σημείο
, στο σημείο  .
.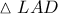 , είναι
, είναι  , και χρησιμοποιώντας την παραλληλία
, και χρησιμοποιώντας την παραλληλία  , προκύπτουν οι γωνίες του σχήματος.
, προκύπτουν οι γωνίες του σχήματος. εγγράψιμο. Επίσης,
εγγράψιμο. Επίσης,  τραπέζιο, και άρα το
τραπέζιο, και άρα το  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο. (1).
(1). (2).
(2). , άρα
, άρα  (3).
(3). , άρα
, άρα  , ό.έ.δ.
, ό.έ.δ.