Δίνονται δύο κύκλοι
Δημοσιεύτηκε: Πέμ Απρ 19, 2018 10:53 pm
Δίνονται δύο κύκλοι  με διάκεντρο μεγαλύτερη από το άθροισμα των ακτινών τους (αυτό απλά το δίνουμε για να έχουμε ανοικτότερο σχήμα) και δύο σημεία
με διάκεντρο μεγαλύτερη από το άθροισμα των ακτινών τους (αυτό απλά το δίνουμε για να έχουμε ανοικτότερο σχήμα) και δύο σημεία  των
των  αντίστοιχα. Βρείτε τον γεωμετρικό τόπο των σημείων
αντίστοιχα. Βρείτε τον γεωμετρικό τόπο των σημείων  του επιπέδου των κύκλων που έχουν την ιδιότητα
του επιπέδου των κύκλων που έχουν την ιδιότητα 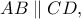 αν
αν 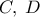 είναι τα άλλα σημεία τομής των
είναι τα άλλα σημεία τομής των 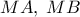 με τους κύκλους
με τους κύκλους  αντίστοιχα.
αντίστοιχα.
 με διάκεντρο μεγαλύτερη από το άθροισμα των ακτινών τους (αυτό απλά το δίνουμε για να έχουμε ανοικτότερο σχήμα) και δύο σημεία
με διάκεντρο μεγαλύτερη από το άθροισμα των ακτινών τους (αυτό απλά το δίνουμε για να έχουμε ανοικτότερο σχήμα) και δύο σημεία  των
των  αντίστοιχα. Βρείτε τον γεωμετρικό τόπο των σημείων
αντίστοιχα. Βρείτε τον γεωμετρικό τόπο των σημείων  του επιπέδου των κύκλων που έχουν την ιδιότητα
του επιπέδου των κύκλων που έχουν την ιδιότητα 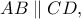 αν
αν 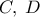 είναι τα άλλα σημεία τομής των
είναι τα άλλα σημεία τομής των 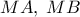 με τους κύκλους
με τους κύκλους  αντίστοιχα.
αντίστοιχα. να είναι κοινή εξωτερική τους εφαπτομένη.
να είναι κοινή εξωτερική τους εφαπτομένη.  τα κέντρα των δύο κύκλων και
τα κέντρα των δύο κύκλων και  το σταθερό σημείο τομής των
το σταθερό σημείο τομής των 
 φέρνω παράλληλη στην
φέρνω παράλληλη στην  όπως φαίνεται στο σχήμα.
όπως φαίνεται στο σχήμα.  το σταθερό σημείο τομής των
το σταθερό σημείο τομής των  και έστω
και έστω 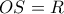 .Tο σημείο
.Tο σημείο 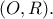
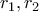 οι ακτίνες των κύκλων
οι ακτίνες των κύκλων 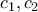 αντίστοιχα. Θεωρούμε τον κύκλο
αντίστοιχα. Θεωρούμε τον κύκλο  , ακτίνας
, ακτίνας  που είναι περιγεγραμμένος στο τρίγωνο
που είναι περιγεγραμμένος στο τρίγωνο  Παρατηρούμε ότι
Παρατηρούμε ότι  με
με 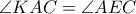 , αφού η γωνία
, αφού η γωνία 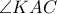 είναι η υπό χορδής και εφαπτομένης σχηματιζόμενη και η γωνία
είναι η υπό χορδής και εφαπτομένης σχηματιζόμενη και η γωνία 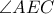 είναι η αντίστοιχη εγγεγραμμένη. Όμως οι γωνίες
είναι η αντίστοιχη εγγεγραμμένη. Όμως οι γωνίες 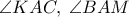 είναι ίσες ως κατακορυφή και
είναι ίσες ως κατακορυφή και 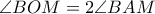 . Συνεπώς από τις προηγούμενες σχέσεις παίρνουμε
. Συνεπώς από τις προηγούμενες σχέσεις παίρνουμε 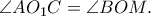 Τα ισοσκελή λοιπόν τρίγωνα
Τα ισοσκελή λοιπόν τρίγωνα 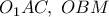 είναι όμοια. Με τον ίδιο τρόπο αποδεικνύεται ότι τα τρίγωνα
είναι όμοια. Με τον ίδιο τρόπο αποδεικνύεται ότι τα τρίγωνα  είναι όμοια. Τελικά έχουμε
είναι όμοια. Τελικά έχουμε 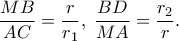 Πολλαπλασιάζουμε τις σχέσεις αυτές κατά μέλη και παίρνουμε
Πολλαπλασιάζουμε τις σχέσεις αυτές κατά μέλη και παίρνουμε  με
με 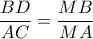 από το θεώρημα του Θαλή. Τελικά έχουμε
από το θεώρημα του Θαλή. Τελικά έχουμε 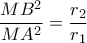 ή
ή 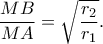
 , με λόγο
, με λόγο 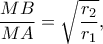 που προφανώς είναι σταθερός.
που προφανώς είναι σταθερός.