 με
με  και
και  το μέσον της πλευράς
το μέσον της πλευράς  . Στην προέκταση της
. Στην προέκταση της  παίρνουμε
παίρνουμε 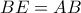 .
. H
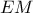 τέμνει την
τέμνει την  στο
στο  και την διχοτόμο
και την διχοτόμο  στο
στο  . Έστω
. Έστω  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Αν είναι
. Αν είναι 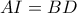 τότε
τότε Να εξεταστεί αν ισχύει :
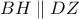
Ευχαριστώ , Γιώργος .
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 με
με  και
και  το μέσον της πλευράς
το μέσον της πλευράς  . Στην προέκταση της
. Στην προέκταση της  παίρνουμε
παίρνουμε 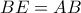 .
. 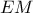 τέμνει την
τέμνει την  στο
στο  και την διχοτόμο
και την διχοτόμο  στο
στο  . Έστω
. Έστω  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Αν είναι
. Αν είναι 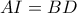 τότε
τότε 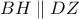
Καλημέρα σε όλους! ΈστωΓιώργος Μήτσιος έγραψε:Καλημέρα -μετά από καιρό- σε όλους!
3-9-17 Χρυσή παραλληλία.PNG
Δίνεται τρίγωνομε
και
το μέσον της πλευράς
. Στην προέκταση της
παίρνουμε
.
Hτέμνει την
στο
και την διχοτόμο
στο
. Έστω
το συμμετρικό του
ως προς το
. Αν είναι
τότε
Να εξεταστεί αν ισχύει :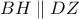
Ευχαριστώ , Γιώργος .
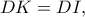 όπως φαίνεται στο σχήμα. Οπότε,
όπως φαίνεται στο σχήμα. Οπότε, 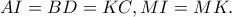
 θα είναι ως γνωστόν
θα είναι ως γνωστόν 
 Είναι ακόμα:
Είναι ακόμα: 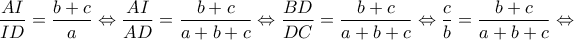



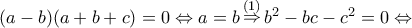
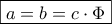 ,
, 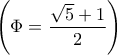
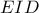 με διατέμνουσα
με διατέμνουσα 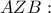
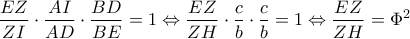


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες