 . Στη διχοτόμο
. Στη διχοτόμο  παίρνουμε
παίρνουμετμήματα :
 . Οι
. Οι  τέμνουν την
τέμνουν την  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .Υπολογίστε το λόγο :
 .
.Βρείτε τη μικρότερη ακέραια τιμή του
 , ώστε το μήκος του
, ώστε το μήκος του  να είναι επίσης ακέραιος .
να είναι επίσης ακέραιος .Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 . Στη διχοτόμο
. Στη διχοτόμο  παίρνουμε
παίρνουμε . Οι
. Οι  τέμνουν την
τέμνουν την  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα . .
. , ώστε το μήκος του
, ώστε το μήκος του  να είναι επίσης ακέραιος .
να είναι επίσης ακέραιος . έχω
έχω  συνεπώς
συνεπώς  Τώρα με Θ. Μενελάου στο
Τώρα με Θ. Μενελάου στο  και
και  έχω :
έχω : και μετά εύκολα
και μετά εύκολα  .
. 
 έχω
έχω  και άρα με
και άρα με  έχω
έχω 
 )
)Να συγχαρώ για μία ακόμη φορά τον Θανάση, για τις πολύ ωραίες ασκήσεις που μας τροφοδοτείKARKAR έγραψε:Πες τον καλό το λόγο.pngΤο τρίγωνο του σχήματος είναι τύπου :. Στη διχοτόμο
παίρνουμε
τμήματα :. Οι
τέμνουν την
στα σημεία
αντίστοιχα .
Υπολογίστε το λόγο :.
Βρείτε τη μικρότερη ακέραια τιμή του, ώστε το μήκος του
να είναι επίσης ακέραιος .
 Από εδώ έχουμε ότι
Από εδώ έχουμε ότι  άρα
άρα  και επειδή
και επειδή  το
το  είναι το έγκεντρο του τριγώνου, οπότε:
είναι το έγκεντρο του τριγώνου, οπότε: 
 με διατέμνουσα
με διατέμνουσα 


 άρα η ελάχιστη ακέραιη τιμή είναι για
άρα η ελάχιστη ακέραιη τιμή είναι για  δηλαδή
δηλαδή  και
και 

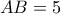 , οπότε
, οπότε  ;
; , το οποίο έχει
, το οποίο έχει και συνεπώς
και συνεπώς  . Αλλά
. Αλλά  , άρα
, άρα 
Πάλι μας εκπλήσσεις (παρόλο ότι πέρασε η Πρωταπριλιά)! Προσωπικά, χωρίς κανένα λόγο θεώρησα ότι οKARKAR έγραψε:Ευχαριστώ τους φίλους Γιώργο και Νίκο για τα καλά τους λόγια , με δύο παρατηρήσεις :
1η) Υπερβολές ... αλλά : 2η) Την Πρωταπριλιά βρήκατε να τα πείτε ?
Τι θα λέγατε να παίρναμε την πλευρά, οπότε
;
Σημείωση : Η άσκηση στηρίχθηκε στο τρίγωνο με πλευρές, το οποίο έχει
διχοτόμοκαι συνεπώς
. Αλλά
, άρα
 είναι ακέραιος.
είναι ακέραιος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες