 θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:
θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:
Συντονιστές: achilleas, emouroukos, silouan
 θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:
θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:

Αν δεν κάνω λάθος εδω μπορούμε να διατάξουμε τις μεταβλητές και μετά εύκολα βγαίνουμε στο ζητουμενο?
Δεν είναι τόσο απλά τα πράγματα. Λόγω κυκλικότητας, δεν μπορούμε να διατάξουμε τις μεταβλητές.telemathic έγραψε: ↑Κυρ Μαρ 19, 2023 10:23 amΑν δεν κάνω λάθος εδω μπορούμε να διατάξουμε τις μεταβλητές και μετά εύκολα βγαίνουμε στο ζητουμενο?

 .
.

 και
και  για κάποιους
για κάποιους  και η αποδεικτέα γίνεται:
και η αποδεικτέα γίνεται: 


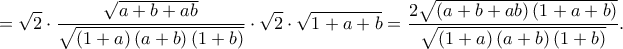



 που αληθεύει .
που αληθεύει . 
Θανο καλησπέρα. Το αναφέρεις ως παράπονο ; Στο
Κανένα παράπονο. Απλή επισήμανση.Henri van Aubel έγραψε: ↑Κυρ Ιουν 25, 2023 6:39 pmΘανο καλησπέρα. Το αναφέρεις ως παράπονο ; Στοκανείς δεν αντιγράφει κανέναν .Νομίζω ότι την έκανα πιο απλή την ανισότητα, εφόσον την μετέτρεψα σε ανισότητα όπου εμπλέκονται 2 μεταβλητές αντί για τρεις .
Α, ok.matha έγραψε: ↑Κυρ Ιουν 25, 2023 7:13 pmΚανένα παράπονο. Απλή επισήμανση.Henri van Aubel έγραψε: ↑Κυρ Ιουν 25, 2023 6:39 pmΘανο καλησπέρα. Το αναφέρεις ως παράπονο ; Στοκανείς δεν αντιγράφει κανέναν .Νομίζω ότι την έκανα πιο απλή την ανισότητα, εφόσον την μετέτρεψα σε ανισότητα όπου εμπλέκονται 2 μεταβλητές αντί για τρεις .
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες