 είναι θετικός ακέραιος ώστε
είναι θετικός ακέραιος ώστε 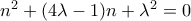 για κάποιο ακέραιο αριθμό
για κάποιο ακέραιο αριθμό  . Να δειχθεί ότι ο
. Να δειχθεί ότι ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.Φιλικά,
Αχιλλέας
Συντονιστές: achilleas, emouroukos, silouan
 είναι θετικός ακέραιος ώστε
είναι θετικός ακέραιος ώστε 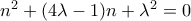 για κάποιο ακέραιο αριθμό
για κάποιο ακέραιο αριθμό  . Να δειχθεί ότι ο
. Να δειχθεί ότι ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.Λύνοντας ως προς
 έχουμε:
έχουμε: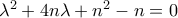
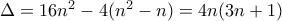
 ακέραιος, αφού ο
ακέραιος, αφού ο  είναι ακέραιος, πρέπει
είναι ακέραιος, πρέπει  άρα η
άρα η  είναι τέλειο τετράγωνο ακεραίου.
είναι τέλειο τετράγωνο ακεραίου.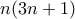 είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο  .
.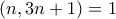 άρα για να ισχύει η
άρα για να ισχύει η  πρέπει οι
πρέπει οι  και
και 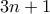 να είναι τέλεια τετράγωνα.
να είναι τέλεια τετράγωνα.Έσβησα μια λύση που είχα γράψει, γιατί είχα παραναγνώσει την εκφώνηση ως
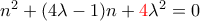 .
.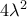 αντί σκέτο
αντί σκέτο  ). Αλλά υπάρχουν περιορισμοί. α) Επειδή η λύση που έγραψε ο Μανώλης (για την σωστή άσκηση) περνάει ατόφια για την νέα μορφή της, ζητώ διαφορετική λύση. β) Επιτρέπεται λύση μόνο της μισής γραμμής. Κάνει για Γυμνάσιο.
). Αλλά υπάρχουν περιορισμοί. α) Επειδή η λύση που έγραψε ο Μανώλης (για την σωστή άσκηση) περνάει ατόφια για την νέα μορφή της, ζητώ διαφορετική λύση. β) Επιτρέπεται λύση μόνο της μισής γραμμής. Κάνει για Γυμνάσιο. Mihalis_Lambrou έγραψε: ↑Σάβ Μαρ 12, 2022 1:55 amΈσβησα μια λύση που είχα γράψει, γιατί είχα παραναγνώσει την εκφώνηση ως.
Λύστε τώρα την άσκηση στην μορφή που μόλις ανέφερα (δηλαδή μεαντί σκέτο
). Αλλά υπάρχουν περιορισμοί. α) Επειδή η λύση που έγραψε ο Μανώλης (για την σωστή άσκηση) περνάει ατόφια για την νέα μορφή της, ζητώ διαφορετική λύση. β) Επιτρέπεται λύση μόνο της μισής γραμμής. Κάνει για Γυμνάσιο.
Με την ευκαιρία θέλω να ευχαριστήσω τον Γενικό Συντονιστή μας Δημήτρη για την επισήμανση του σφάλματός μου. Επίσης προσθέτω ότι η λύση που είχα γράψει δεν ήταν της μισής γραμμής, αλλά "περισσότερη φασαρία" συν τυπογραφικό σφάλμα. Την λύση της μισής γραμμής που ζητώ, την σκέφτηκα αργότερα, καθώς προσπαθούσα να μπαλώσω την αρχική μου λύση.

.
 , τώρα παρελθόν, ήταν
, τώρα παρελθόν, ήταν  είναι
είναι 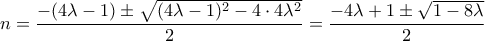 .
. 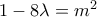 . Ακόμα καλύτερα, αφού το αριστερό μέλος είναι περιττός αριθμός, θα είναι και το
. Ακόμα καλύτερα, αφού το αριστερό μέλος είναι περιττός αριθμός, θα είναι και το  , δηλαδή θα έχουμε
, δηλαδή θα έχουμε 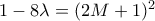 , ισοδύναμα
, ισοδύναμα 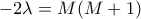 .
. θα δώσει
θα δώσει 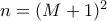 ή
ή 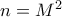 . Αυτό θέλαμε να δείξουμε.
. Αυτό θέλαμε να δείξουμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες