
Να δειχθεί ότι υπάρχουν πραγματικοί

ώστε

για κάθε

Συντονιστές: achilleas, emouroukos, silouan




ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Αύγ 09, 2020 11:15 amΔίνονται οι πραγματικοί
Να δειχθεί ότι υπάρχουν πραγματικοί
ώστε
για κάθε
 Αν
Αν  τότε θέλουμε
τότε θέλουμε  .
. Αν
Αν  , τότε θέλουμε
, τότε θέλουμε  .
. Αν ο ένας είναι θετικός και ο άλλος αρνητικός - έστω χωρίς βλάβη της γενικότητας
Αν ο ένας είναι θετικός και ο άλλος αρνητικός - έστω χωρίς βλάβη της γενικότητας  , τότε θέλουμε
, τότε θέλουμε  , καθώς
, καθώς  .
. και
και 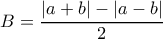 (είναι προφανές ότι αυτά τα
(είναι προφανές ότι αυτά τα  δουλεύουν).
δουλεύουν).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες