
Κλασματική εξίσωση
Συντονιστές: achilleas, emouroukos, silouan
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13275
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: Κλασματική εξίσωση
Καλημέρα!
Αφαιρούμε από κάθε όρο το
 οπότε εξακολουθεί να ισχύει η ισότητα και
οπότε εξακολουθεί να ισχύει η ισότητα και  και ομοίως οι υπόλοιποι όροι οπότε η αρχική γράφεται:
και ομοίως οι υπόλοιποι όροι οπότε η αρχική γράφεται: .
.Για
 δεν μηδενίζεται κάποιος παρονομαστής οπότε λύση της εξίσωσης και τώρα γράφεται:
δεν μηδενίζεται κάποιος παρονομαστής οπότε λύση της εξίσωσης και τώρα γράφεται:


Για
 δεν μηδενίζεται κάποιος παρονομαστής άρα
δεν μηδενίζεται κάποιος παρονομαστής άρα  λύση της εξίσωσης και τώρα:
λύση της εξίσωσης και τώρα:
Στην παραπάνω αφαιρούμε
 από κάθε μέλος και γίνεται
από κάθε μέλος και γίνεται η οποία έχει λύση
η οποία έχει λύση  και για
και για  γράφεται (απλοποιώ με το
γράφεται (απλοποιώ με το  )
) (μιας και δεν δόθηκε περιορισμός
(μιας και δεν δόθηκε περιορισμός  )
)Λύσεις λοιπόν οι
 (διπλή),
(διπλή), και οι
και οι 
Re: Κλασματική εξίσωση
Πολύ ωραία ο Πρόδρομος 
Μια παρεμφερή, Θέτω :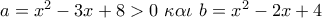 και η εξίσωση γράφεται :
και η εξίσωση γράφεται :
 ή
ή

Τα υπόλοιπα απλά .
Μια παρεμφερή, Θέτω :
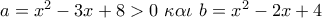 και η εξίσωση γράφεται :
και η εξίσωση γράφεται : ή
ή 
Τα υπόλοιπα απλά .
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13275
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Κλασματική εξίσωση
Αλλιώς, θέτω  και η δοσμένη εξίσωση γράφεται:
και η δοσμένη εξίσωση γράφεται:
 ή
ή 

 ή
ή  ή
ή 
Ομοίως για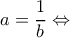
 ή
ή  που δεν έχει πραγματικές ρίζες.
που δεν έχει πραγματικές ρίζες.
Σημείωση: Ο Πρόδρομος καλά έκανε που, για λόγους πληρότητας, συμπεριέλαβε στις ρίζες και τις δύο φανταστικές.
Επειδή όμως οι μιγαδικοί έχουν αφαιρεθεί από την ύλη της Γ Λυκείου και ο φάκελος είναι Θαλής-Ευκλείδης, μπορούμε
να τις απορρίψουμε. Το πιο σωστό βέβαια, θα ήταν να γράψω "Να λυθεί στο η εξίσωση..."
η εξίσωση..."
 και η δοσμένη εξίσωση γράφεται:
και η δοσμένη εξίσωση γράφεται: ή
ή 

 ή
ή  ή
ή 
Ομοίως για
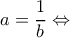
 ή
ή  που δεν έχει πραγματικές ρίζες.
που δεν έχει πραγματικές ρίζες.Σημείωση: Ο Πρόδρομος καλά έκανε που, για λόγους πληρότητας, συμπεριέλαβε στις ρίζες και τις δύο φανταστικές.
Επειδή όμως οι μιγαδικοί έχουν αφαιρεθεί από την ύλη της Γ Λυκείου και ο φάκελος είναι Θαλής-Ευκλείδης, μπορούμε
να τις απορρίψουμε. Το πιο σωστό βέβαια, θα ήταν να γράψω "Να λυθεί στο
 η εξίσωση..."
η εξίσωση..."Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
