Ένας άλλος τρόπος είναι ο «λαίμαργος αλγόριθμος». Θα υποθέσουμε αρχικά ότι το κλάσμα μας ανήκει στο διάστημα

.
Κάθε φορά γράφουμε το μεγαλύτερο εναδικό κλάσμα που δεν υπερβαίνει το κλάσμα που παραμένει. Π.χ.

Σίγουρα δεν γράφουμε ποτέ δυο φορές το ίδιο κλάσμα διότι αν είχαμε γράψει δυο φορές το

θα μπορούσαμε την πρώτη φορά να γράψουμε το

, άτοπο. (Πρέπει

αφού αλλιώς

.)
Για να δείξουμε ότι η διαδικασία τερματίζεται θα δείξουμε ότι στο κλάσμα που παραμένει ο αριθμητής σε κάθε βήμα μειώνεται.
Έστω ότι μένει το κλάσμα

και ότι ακολούθως γράψαμε το κλάσμα

. Αυτό σημαίνει ότι

Το επόμενο κλάσμα που παραμένει είναι το

το οποίο όταν απλοποιηθεί, έχει παρονομαστή μικρότερο ή ίσο του

. Θέλουμε να δείξουμε ότι

. Αυτό όμως είναι ισοδύναμο με το

που γνωρίζουμε ήδη.
Πάμε τώρα να δούμε τι κάνουμε αν αρχίσουμε από ρητό μεγαλύτερο ή ίσο του

.
Πάλι προχωράμε λαίμαργα μόνο που αυτήν την φορά γράφουμε το μεγαλύτερο εναδικό κλάσμα που δεν υπερβαίνει το κλάσμα που παραμένει και το οποίο δεν έχουμε ήδη γράψει. Η ίδια ουσιαστικά απόδειξη δουλεύει και πάλι μόνο που αυτήν την φορά ο αριθμητής μειώνεται από ένα σημείο και μετά. Το σημείο που σίγουρα αρχίζει να μειώνεται είναι όταν γράψουμε το κλάσμα

ενώ το κλάσμα που παραμένει είναι μικρότερο του

. Αυτό σίγουρα θα συμβεί επειδή η αρμονική σειρά αποκλίνει.
 (τα λεγόμενα εναδικά κλάσματα).
(τα λεγόμενα εναδικά κλάσματα).  υπάρχει πίνακας με ανάλυσή τους
υπάρχει πίνακας με ανάλυσή τους  στον αρχαίο Αιγυπτιακό πάπυρο Rhind πριν από
στον αρχαίο Αιγυπτιακό πάπυρο Rhind πριν από  χρόνια. Γι΄αυτό τα εναδικά κλάσματα ονομάζονται και Αιγυπτιακά.
χρόνια. Γι΄αυτό τα εναδικά κλάσματα ονομάζονται και Αιγυπτιακά. 
 γράφουμε (επιτρέποντας προσωρινά τις επαναλήψεις)
γράφουμε (επιτρέποντας προσωρινά τις επαναλήψεις)  .
.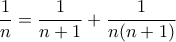 , αν χρειαστεί, διώχνουμε τους όρους που επαναλαμβάνονται, μέχρι που να εξαφανιστούν οι επαναλήψεις. Για παράδειγμα
, αν χρειαστεί, διώχνουμε τους όρους που επαναλαμβάνονται, μέχρι που να εξαφανιστούν οι επαναλήψεις. Για παράδειγμα 

 .
. 
 θα μπορούσαμε την πρώτη φορά να γράψουμε το
θα μπορούσαμε την πρώτη φορά να γράψουμε το  , άτοπο. (Πρέπει
, άτοπο. (Πρέπει  αφού αλλιώς
αφού αλλιώς  .)
.) και ότι ακολούθως γράψαμε το κλάσμα
και ότι ακολούθως γράψαμε το κλάσμα  . Αυτό σημαίνει ότι
. Αυτό σημαίνει ότι 
 το οποίο όταν απλοποιηθεί, έχει παρονομαστή μικρότερο ή ίσο του
το οποίο όταν απλοποιηθεί, έχει παρονομαστή μικρότερο ή ίσο του  . Θέλουμε να δείξουμε ότι
. Θέλουμε να δείξουμε ότι  . Αυτό όμως είναι ισοδύναμο με το
. Αυτό όμως είναι ισοδύναμο με το  που γνωρίζουμε ήδη.
που γνωρίζουμε ήδη. .
. ενώ το κλάσμα που παραμένει είναι μικρότερο του
ενώ το κλάσμα που παραμένει είναι μικρότερο του