Αν
 με
με  , αποδείξτε ότι
, αποδείξτε ότι 
Συντονιστές: achilleas, emouroukos, silouan
 με
με  , αποδείξτε ότι
, αποδείξτε ότι 
Καλησπέρα σας!ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Πέμ Οκτ 26, 2017 2:42 pmΣήμερα σας προτείνω το θέμα 146 από το αρχείο του Θάνου.Το έλυσα την Τρίτη το πρωί σε ένα κενό στο σχολείο...
Ανμε
, αποδείξτε ότι

 . Αρα αρκεί μετά από παραγοντοποίηση
. Αρα αρκεί μετά από παραγοντοποίηση  . Με χρήση της
. Με χρήση της  και πολλαπλασιάζοντας με
και πολλαπλασιάζοντας με 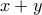 έχουμε
έχουμε 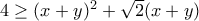 που ισχύει αφού
που ισχύει αφού  .
. και αφού
και αφού  το ζητούμενο είναι προφανές.
το ζητούμενο είναι προφανές.Μπορούμε ουσιαστικά να την λάβουμε αμέσως από την πρώτη ανισότητα αν θέσουμε
 και
και  .
.Ας δοκιμάσουμε ομογενοποίηση. Αρκεί να δείξουμε ότι

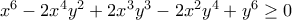
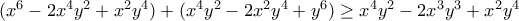

 που προφανώς ισχύει.
που προφανώς ισχύει.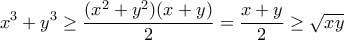 (γιατί;), οπότε αρκεί
(γιατί;), οπότε αρκεί  δηλαδή
δηλαδή 

 και
και  με
με  Αρκεί
Αρκεί 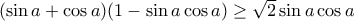
 και υψώνοντας στο τετράγωνο
και υψώνοντας στο τετράγωνο και θέτοντας
και θέτοντας  αρκεί
αρκεί ή
ή που προφανώς ισχύει.
που προφανώς ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες