Νομίζω ότι η λύση έχει πολλά προβλήματα. Ένα είναι αυτό:
KARKAR έγραψε: ↑Πέμ Απρ 02, 2020 11:31 am
Μπορούμε να αποφύγουμε τις παραπάνω δυσκολίες , βρίσκοντας εκείνο το

, για το οποίο
το πολυώνυμο έχει μία απλή ρίζα ( έστω

) και μία διπλή ρίζα ( έστω

) .
Η άρνηση της πρότασης "μοναδική ρίζα" που ζητά η άσκηση, δεν είναι το παραπάνω αλλά η πρόταση "έχει τρεις
ρίζες, μετρώντας και την πολλαπλότητα". Δηλαδή επιτρέπεται τριπλή ρίζα και (κυρίως) επιτρέπονται
τρεις διαφορετικές. Από που προκύπτει ότι το

που περιγράφεται παραπάνω είναι το ζητούμενο;
Ένα δεύτερο πρόβλημα είναι εδώ:
KARKAR έγραψε: ↑Πέμ Απρ 02, 2020 1:11 pm
μεταβάλλεται μόνο κατά το τμήμα

, το οποίο
αυξάνει καθώς το

αυξάνει .
Τι γίνεται με τα αρνητικά

; Εκεί το

μειώνεται. Υπόψη ότι η περίπτωση αυτή είναι υπαρκτή. Π.χ. για

έχουμε ακριβώς μία πραγματική ρίζα, όπως μπορούμε να ελέγξουμε απευθείας (σχεδίασα άλλωστε το
γράφημα με λογισμικό).
Όλα αυτά διορθώνονται, αλλά τότε ξεφύγαμε από την απλότητα.
 , για το οποίο η εξίσωση
, για το οποίο η εξίσωση 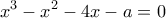 έχει τρεις διαφορετικές μεταξύ τους ρίζες, συμβολίζουμε με
έχει τρεις διαφορετικές μεταξύ τους ρίζες, συμβολίζουμε με  αυτές τις ρίζες διατεταγμένες κατά φθίνουσα σειρά
αυτές τις ρίζες διατεταγμένες κατά φθίνουσα σειρά  . Προσδιορίστε, για ποιό από αυτά τα
. Προσδιορίστε, για ποιό από αυτά τα  η έκφραση
η έκφραση  λαμβάνει την μέγιστη δυνατή τιμή της.
λαμβάνει την μέγιστη δυνατή τιμή της.
 είναι αναδιάταξη των
είναι αναδιάταξη των  ποιος είναι ο μικρότερος δυνατός βαθμός που μπορεί να έχει το πολυώνυμο
ποιος είναι ο μικρότερος δυνατός βαθμός που μπορεί να έχει το πολυώνυμο  ;
; .
.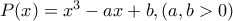 το οποίο έχει τρεις πραγματικές ρίζες. Να αποδείξετε ότι
το οποίο έχει τρεις πραγματικές ρίζες. Να αποδείξετε ότι
 δεν είναι ρίζα αφού
δεν είναι ρίζα αφού  .
. , σημαίνει ότι είτε έχουμε τρεις (γνήσια) αρνητικές ρίζες ή δύο θετικές και μία αρνητική. Αφού το άθροισμα των ριζών είναι
, σημαίνει ότι είτε έχουμε τρεις (γνήσια) αρνητικές ρίζες ή δύο θετικές και μία αρνητική. Αφού το άθροισμα των ριζών είναι  οι δύο θετικές ρίζες, οπότε η αρνητική είναι η
οι δύο θετικές ρίζες, οπότε η αρνητική είναι η  . Άρα από Vieta είναι
. Άρα από Vieta είναι 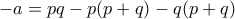 και
και 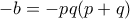 οπότε
οπότε  και
και 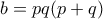 .
. 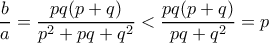 , δηλαδή το ένα ζητούμενο. Και
, δηλαδή το ένα ζητούμενο. Και  , όπως θέλαμε.
, όπως θέλαμε. : Η αρχική δίνει για οποιαδήποτε από τις θετικές ρίζες
: Η αρχική δίνει για οποιαδήποτε από τις θετικές ρίζες  , άρα
, άρα 
 , για την οποία για κάθε
, για την οποία για κάθε  το πολυώνυμο
το πολυώνυμο  , έχει ακριβώς μία πραγματική ρίζα .
, έχει ακριβώς μία πραγματική ρίζα . . Πρόκειται για άσκηση χωρίς φαντασία, στάνταρ στη θεωρία τριτοβάθμιων, με πολλές πράξεις.
. Πρόκειται για άσκηση χωρίς φαντασία, στάνταρ στη θεωρία τριτοβάθμιων, με πολλές πράξεις. , οπότε η διακρίνουσα είναι
, οπότε η διακρίνουσα είναι  . Εδώ ο μετασχηματισμός
. Εδώ ο μετασχηματισμός  φέρνει την αρχική στην μορφή
φέρνει την αρχική στην μορφή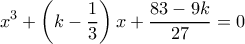
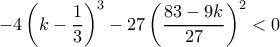
 (το έχω ελέγξει μία φορά αλλά δεν αντέχω δεύτερη). Επειδή ο δευτεροβάθμιος όρος στην παρένθεση είναι θετικός, θέλουμε
(το έχω ελέγξει μία φορά αλλά δεν αντέχω δεύτερη). Επειδή ο δευτεροβάθμιος όρος στην παρένθεση είναι θετικός, θέλουμε 
 ) και μία διπλή ρίζα ( έστω
) και μία διπλή ρίζα ( έστω  ) .
) . και
και  .
.
 . Άρα θέλουμε :
. Άρα θέλουμε : 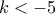 .
. , το οποίο έχει μια απλή
, το οποίο έχει μια απλή 
 , το οποίο αυξάνει καθώς το
, το οποίο αυξάνει καθώς το  αυξάνει .
αυξάνει . έχουμε ακριβώς μία πραγματική ρίζα, όπως μπορούμε να ελέγξουμε απευθείας (σχεδίασα άλλωστε το
έχουμε ακριβώς μία πραγματική ρίζα, όπως μπορούμε να ελέγξουμε απευθείας (σχεδίασα άλλωστε το πραγματικοί αριθμοί με
πραγματικοί αριθμοί με  και έστω
και έστω  . Δείξτε ότι
. Δείξτε ότι 
 άρα η εξίσωση
άρα η εξίσωση  έχει πραγματική ρίζα (την
έχει πραγματική ρίζα (την  ), άρα μη αρνητική διακρίνουσα.
), άρα μη αρνητική διακρίνουσα. αφού
αφού 
 , τότε όμως έχουμε να δείξουμε ότι
, τότε όμως έχουμε να δείξουμε ότι 
 .
. πρέπει
πρέπει  .
. .
. δίνουν
δίνουν  .
. περιλαμβάνεται στην
περιλαμβάνεται στην 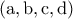 χωρίς βλάβη θέτω
χωρίς βλάβη θέτω  .
. .Έστω
.Έστω  .
. θα είναι
θα είναι  .
. τότε
τότε  άτοπο.Άρα
άτοπο.Άρα  και
και  που εύκολα δίνει
που εύκολα δίνει  .
. και
και 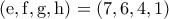 (ή κάποια αναδιάταξη,δεν έχει σημασία λόγω συμμετρίας).
(ή κάποια αναδιάταξη,δεν έχει σημασία λόγω συμμετρίας). άρα ο ελάχιστος βαθμός του πολυωνύμου είναι ο
άρα ο ελάχιστος βαθμός του πολυωνύμου είναι ο  .
. για
για  .
. δύο πολυώνυμα με πραγματικούς συντελεστές τέτοια ώστε για κάθε πραγματικό
δύο πολυώνυμα με πραγματικούς συντελεστές τέτοια ώστε για κάθε πραγματικό  ισχύει
ισχύει 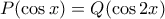 .
.  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε  και
και  .
. παίρνουμε
παίρνουμε 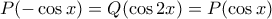 , δηλαδή μία ισότητα της μορφής
, δηλαδή μία ισότητα της μορφής  έστω για κάποια
έστω για κάποια  .
.  λαμβάνουμε
λαμβάνουμε  δηλαδή ισχύει
δηλαδή ισχύει 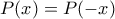 για άπειρες τιμές του
για άπειρες τιμές του  , άρα για κάθε
, άρα για κάθε 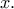 Δηλαδή το
Δηλαδή το  είναι άρτιο πολυώνυμο, οπότε υπάρχει πολυώνυμο
είναι άρτιο πολυώνυμο, οπότε υπάρχει πολυώνυμο  , ώστε
, ώστε 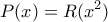 . Τότε η συνθήκη γίνεται
. Τότε η συνθήκη γίνεται  , οπότε ισχύει
, οπότε ισχύει για άπειρες τιμές του
για άπειρες τιμές του  πολυώνυμο με πραγματικούς συντελεστές συντελεστές τέτοιο ώστε
πολυώνυμο με πραγματικούς συντελεστές συντελεστές τέτοιο ώστε  . Δείξτε ότι υπάρχουν πραγματικοί αριθμοί
. Δείξτε ότι υπάρχουν πραγματικοί αριθμοί  τέτοιοι ώστε
τέτοιοι ώστε  και
και 
