Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 05, 2023 7:07 pm
Άσκηση 50
'Εστω  μονικό πολυώνυμο πέμπτου βαθμού με πέντε διαφορετικές πραγματικές ρίζες
μονικό πολυώνυμο πέμπτου βαθμού με πέντε διαφορετικές πραγματικές ρίζες  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.
Edit: Πρόσθεσα δύο λέξεις για να μην υπάρχει αμφιβολία για το τι ακριβώς πολυώνυμο συζητάμε.
Για λόγους πληρότητας γράφω την λύση αναλυτικότερα, και με την διευκρίνιση ότι το πολυώνυμο είναι πέμπτου βαθμού. Δεν λέω τίποτα καινούργιο αλλά απλά καθαρογράφω τις δύο ήδη αναφερθείσες λύσεις. Αυτό που μου αρέσει στην άσκηση (και γι' αυτό την ανάρτησα) είναι το τέχνασμα που αναφέρει ο Σταύρος στην πέμπτη γραμμή του ποστ του.
Χωρίς βλάβη οι ρίζες ικανοποιούν

. Θα δείξουμε ότι α)

, β)

, γ)

Έχουμε

, από όπου εύκολα βρίσκουμε το

(ως κάποιο άθροισμα με πέντε προσθετέους. Άρα
το β) είναι άμεσο:

Για το α)

![=(x_2-x_1) \left [ (x_3-x_1)(x_4-x_1)(x_5-x_1) - (x_3-x_2)(x_4-x_2)(x_5-x_2) \right ] =(x_2-x_1) \left [ (x_3-x_1)(x_4-x_1)(x_5-x_1) - (x_3-x_2)(x_4-x_2)(x_5-x_2) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7328f96f7a715d848074ee84c12bdcc2.png)
Εδώ ο πρώτος (και κοινός) παράγοντας

είναι
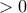
. Επίσης η παράσταση μέσα στις
![[.] [.]](/forum/ext/geomar/texintegr/latexrender/pictures/d0b10a15db40a36d59fddb83ef024cf2.png)
είναι θετική διότι
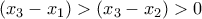
και

και

. Πολλαπλασιάζουμε τώρα κατά μέλη, από όπου το ζητούμενο.
Για το γ) εργαζόμαστε ακριβώς όπως στο

αλλά βγάζοντας τον κοινό παράγοντα

. Τελειώσαμε.
 , όμως αριστερά έχουμε περιττό, άρα αναγκαστικά και δεξιά, άρα κρατάμε το 5 (άρα πάνω έχουμε το 10), άρα το πρόσημο του
, όμως αριστερά έχουμε περιττό, άρα αναγκαστικά και δεξιά, άρα κρατάμε το 5 (άρα πάνω έχουμε το 10), άρα το πρόσημο του  είναι
είναι  . Συνεχίζοντας:
. Συνεχίζοντας:  και πάλι
και πάλι  κρατάμε το
κρατάμε το  άρα το πρόσημο του
άρα το πρόσημο του  είναι
είναι  .
. , κρατάμε το
, κρατάμε το  άρα το πρόσημο του
άρα το πρόσημο του  είναι
είναι  .
.  κρατάμε το
κρατάμε το  άρα το πρόσημο του
άρα το πρόσημο του  είναι
είναι  .
. 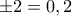 , άρα το πρόσημο του
, άρα το πρόσημο του  είναι
είναι  . Γνωρίζουμε τους συντελεστές όλων των όρων εκτός του
. Γνωρίζουμε τους συντελεστές όλων των όρων εκτός του  άρα "βάζουμε" στο πολυώνυμο το
άρα "βάζουμε" στο πολυώνυμο το  και βρίσκουμε ότι το πρόσημο του
και βρίσκουμε ότι το πρόσημο του  είναι
είναι  . Τελικά το ζητούμενο πολυώνυμο είναι το
. Τελικά το ζητούμενο πολυώνυμο είναι το  .
.
 είναι της μορφής
είναι της μορφής  για κάποια επολογή των προσήμων. Αν
για κάποια επολογή των προσήμων. Αν  , να βρεθεί πολυώνυμο.
, να βρεθεί πολυώνυμο. (διότι το δεξί μέλος ισούται
(διότι το δεξί μέλος ισούται  ) έπεται ότι αθροίσματα της μορφής
) έπεται ότι αθροίσματα της μορφής 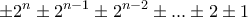 έχουν το πρόσημο του πρώτου όρου. Έτσι η
έχουν το πρόσημο του πρώτου όρου. Έτσι η 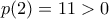 ή αλλιώς
ή αλλιώς 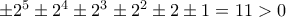 δίνει ότι ο πρώτος όρος είναι
δίνει ότι ο πρώτος όρος είναι  . Έχουμε δηλαδή
. Έχουμε δηλαδή  οπότε και
οπότε και 
 , οπότε τώρα
, οπότε τώρα  . Και ξανά, ο πρώτος όρος είναι
. Και ξανά, ο πρώτος όρος είναι  , οπότε
, οπότε  . Και λοιπά. Τελικά το πολυώνυμο είναι το
. Και λοιπά. Τελικά το πολυώνυμο είναι το  .
. όλοι οι συντελεστές ανήκουν στο σύνολο
όλοι οι συντελεστές ανήκουν στο σύνολο  .
. 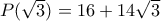 .
.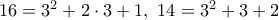
 και
και 
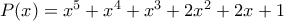
 .
. και
και  ,
,  τότε:
τότε:




 και παρατηρώ ότι το
και παρατηρώ ότι το  είναι πολυώνυμο με συντελεστές στο
είναι πολυώνυμο με συντελεστές στο 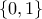 . Επειδή
. Επειδή  τότε
τότε  και άρα
και άρα  .
.
 , έχει ρίζα τον πραγματικό
, έχει ρίζα τον πραγματικό  , υπολογίστε
, υπολογίστε .
. , για κάποια
, για κάποια  . H παράσταση τότε γράφεται
. H παράσταση τότε γράφεται
 (τα υπόλοιπα απλοποιήθηκαν μετά τις πράξεις).
(τα υπόλοιπα απλοποιήθηκαν μετά τις πράξεις).
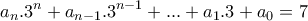 , (ΣΧΕΣΗ 1)
, (ΣΧΕΣΗ 1) , (ΣΧΕΣΗ 2)
, (ΣΧΕΣΗ 2)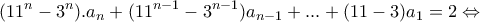
 , όπου οι αριθμοί
, όπου οι αριθμοί  είναι ακέραιοι
είναι ακέραιοι .
.  μιγαδική πέμπτη ρίζα της μονάδας, να αποδείξετε ότι υπάρχουν πολυώνυμα
μιγαδική πέμπτη ρίζα της μονάδας, να αποδείξετε ότι υπάρχουν πολυώνυμα  με ακέραιους συντελεστές τέτοια ώστε
με ακέραιους συντελεστές τέτοια ώστε 
 . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. έχει
έχει  πραγματικές ρίζες τότε αν
πραγματικές ρίζες τότε αν  οι ρίζες του ισχύει
οι ρίζες του ισχύει  , άρα για τη παράγωγο του ισχύει:
, άρα για τη παράγωγο του ισχύει:![P'(x)=[(x-a)(x-b)(x-c)(x-d)(x-e)]' = (x-b)(x-c)(x-d)(x-e) + (x-a)(x-c)(x-d)(x-e) + (x-a)(x-b)(x-d)(x-e) + (x-a)(x-b)(x-c)(x-e) + (x-a)(x-b)(x-c)(x-d) P'(x)=[(x-a)(x-b)(x-c)(x-d)(x-e)]' = (x-b)(x-c)(x-d)(x-e) + (x-a)(x-c)(x-d)(x-e) + (x-a)(x-b)(x-d)(x-e) + (x-a)(x-b)(x-c)(x-e) + (x-a)(x-b)(x-c)(x-d)](/forum/ext/geomar/texintegr/latexrender/pictures/d27a39e39ce61d7c4c6306aebbb26ae2.png)
 και αρκεί να δείξουμε ότι αυτό είναι μη αρνητικό, δηλαδή ότι
και αρκεί να δείξουμε ότι αυτό είναι μη αρνητικό, δηλαδή ότι  Η ανισότητα
Η ανισότητα 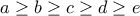 . Έχουμε
. Έχουμε ![(a-b)(a-c)(a-d)(a-e) + (b-a)(b-c)(b-d)(b-e) + (c-a)(c-b)(c-d)(c-e) + (d-a)(d-b)(d-c)(d-e) = (a-b)[(a-c)(a-d)(a-e) - (b-c)(b-d)(b-e)] + (c-d)[(c-a)(c-b)(c-e) - (d-a)(d-b)(d-e)] + (e-a)(e-b)(e-c)(e-d) \ge 0 (a-b)(a-c)(a-d)(a-e) + (b-a)(b-c)(b-d)(b-e) + (c-a)(c-b)(c-d)(c-e) + (d-a)(d-b)(d-c)(d-e) = (a-b)[(a-c)(a-d)(a-e) - (b-c)(b-d)(b-e)] + (c-d)[(c-a)(c-b)(c-e) - (d-a)(d-b)(d-e)] + (e-a)(e-b)(e-c)(e-d) \ge 0](/forum/ext/geomar/texintegr/latexrender/pictures/bc6309846fdc71cb77577f108b40590e.png) αφού
αφού  , άρα το ζητούμενο άθροισμα είναι μη αρνητικό και τελειώσαμε.
, άρα το ζητούμενο άθροισμα είναι μη αρνητικό και τελειώσαμε.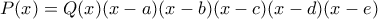 όπου
όπου  μονικό πολυώνυμο,
μονικό πολυώνυμο,
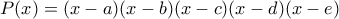 , δηλαδή
, δηλαδή  , και έτσι γλιτώνουμε κάποιες πράξεις.
, και έτσι γλιτώνουμε κάποιες πράξεις.




 δεν αλλάζει αν
δεν αλλάζει αν 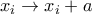 )
)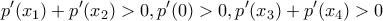


 . Θα δείξουμε ότι α)
. Θα δείξουμε ότι α)  , β)
, β)  , γ)
, γ) 
 , από όπου εύκολα βρίσκουμε το
, από όπου εύκολα βρίσκουμε το  (ως κάποιο άθροισμα με πέντε προσθετέους. Άρα
(ως κάποιο άθροισμα με πέντε προσθετέους. Άρα 

![=(x_2-x_1) \left [ (x_3-x_1)(x_4-x_1)(x_5-x_1) - (x_3-x_2)(x_4-x_2)(x_5-x_2) \right ] =(x_2-x_1) \left [ (x_3-x_1)(x_4-x_1)(x_5-x_1) - (x_3-x_2)(x_4-x_2)(x_5-x_2) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7328f96f7a715d848074ee84c12bdcc2.png)
 είναι
είναι 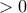 . Επίσης η παράσταση μέσα στις
. Επίσης η παράσταση μέσα στις ![[.] [.]](/forum/ext/geomar/texintegr/latexrender/pictures/d0b10a15db40a36d59fddb83ef024cf2.png) είναι θετική διότι
είναι θετική διότι 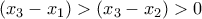 και
και  και
και  . Πολλαπλασιάζουμε τώρα κατά μέλη, από όπου το ζητούμενο.
. Πολλαπλασιάζουμε τώρα κατά μέλη, από όπου το ζητούμενο. αλλά βγάζοντας τον κοινό παράγοντα
αλλά βγάζοντας τον κοινό παράγοντα  . Τελειώσαμε.
. Τελειώσαμε. για κάθε
για κάθε  , όπου
, όπου  οι αριθμοί Fibonacci
οι αριθμοί Fibonacci (άτοπο). Μπορούμε λοιπόν να χαλαρώσουμε την εκφώνηση:
(άτοπο). Μπορούμε λοιπόν να χαλαρώσουμε την εκφώνηση: και πέρα όπου
και πέρα όπου