Ωραία η λύση του Θάνου. Δίνω μία διαφορετική:Mihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 16
Ικανή και αναγκαία συνθήκη για να είναι οι ρίζες τηςσε γεωμετρική πρόοδο είναι
.
Έστω
 οι ρίζες με
οι ρίζες με  . Από Vieta
. Από Vieta  , άρα
, άρα  , οπότε
, οπότε και λοιπά.
και λοιπά. Για το αντίστροφο, παρόμοια, αλλά το αφήνω γιατί οι πράξεις είναι πολλές.

 έχουν γινόμενο όσο οι άλλες δύο, δείξτε ότι
έχουν γινόμενο όσο οι άλλες δύο, δείξτε ότι  .
.  οι ρίζες.
οι ρίζες. (
( ) οπότε
) οπότε  (
( ).
).


 και
και  έχουν κοινή ρίζα, δείξτε
έχουν κοινή ρίζα, δείξτε  .
.  ,
, και κάνοντας την διαίρεση έχουμε
και κάνοντας την διαίρεση έχουμε 




 και κάνουμε τις πράξεις θα προκύψει η ζητούμενη.
και κάνουμε τις πράξεις θα προκύψει η ζητούμενη. μια κοινή ρίζα των δύο εξισώσεων.Τότε, είναι
μια κοινή ρίζα των δύο εξισώσεων.Τότε, είναι 

 βρίσκουμε ότι
βρίσκουμε ότι
 Αν
Αν  , τότε είναι
, τότε είναι 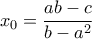
 έχουμε ότι
έχουμε ότι


 , τότε υποχρεωτικά θα είναι και
, τότε υποχρεωτικά θα είναι και  οπότε
οπότε
 έχει ρίζες
έχει ρίζες  , δείξτε ότι
, δείξτε ότι


 .
.
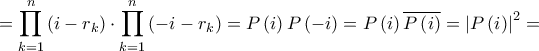
![\displaystyle = {\left[ {{\mathop{\rm Re}\nolimits} \left( {P\left( i \right)} \right)} \right]^2} + {\left[ {{\mathop{\rm Im}\nolimits} \left( {P\left( i \right)} \right)} \right]^2} \displaystyle = {\left[ {{\mathop{\rm Re}\nolimits} \left( {P\left( i \right)} \right)} \right]^2} + {\left[ {{\mathop{\rm Im}\nolimits} \left( {P\left( i \right)} \right)} \right]^2}](/forum/ext/geomar/texintegr/latexrender/pictures/2e1e32ea992414cf07ef05a3b237de9a.png)
 είναι μια κοινή ρίζα, τότε
είναι μια κοινή ρίζα, τότε , οπότε
, οπότε  και
και

 οι ρίζες της εξίσωσης. Υποθέτουμε ότι
οι ρίζες της εξίσωσης. Υποθέτουμε ότι  . Τότε, από τους τύπους του Vieta έχουμε ότι:
. Τότε, από τους τύπους του Vieta έχουμε ότι: ,
,





 είναι ίση με το άθροισμα των άλλων τριών, δείξτε ότι
είναι ίση με το άθροισμα των άλλων τριών, δείξτε ότι 
 , για τις οποίες το πολυώνυμο :
, για τις οποίες το πολυώνυμο :  , έχει τέσσερις διαφορετικές πραγματικές ρίζες .
, έχει τέσσερις διαφορετικές πραγματικές ρίζες . όπου
όπου  οι ρίζες της
οι ρίζες της  . Οπότε για να έχουμε
. Οπότε για να έχουμε  διαφορετικές πραγματικές ρίζες πρέπει
διαφορετικές πραγματικές ρίζες πρέπει  και
και  .
.  να ικανοποιεί
να ικανοποιεί (δευτεροβάθμια)
(δευτεροβάθμια) , ισοδύναμα μεταξύ των
, ισοδύναμα μεταξύ των 
 , ισοδύναμα
, ισοδύναμα  ή
ή 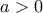
 , ισοδύναμα
, ισοδύναμα  ή
ή 
 .
.
 οπότε από Vieta είναι
οπότε από Vieta είναι  .
.  αυτό πίσω στην εξίσωση, δίνει το ζητούμενο.
αυτό πίσω στην εξίσωση, δίνει το ζητούμενο.