socrates έγραψε: ↑Τρί Απρ 14, 2020 12:35 amMihalis_Lambrou έγραψε: ↑Τρί Απρ 14, 2020 12:27 amΆσκηση 40
Έστωπολυώνυμο με πραγματικούς συντελεστές συντελεστές τέτοιο ώστε
. Δείξτε ότι υπάρχουν πραγματικοί αριθμοί
τέτοιοι ώστε
και
Η σωστή λύση είναι δυο-τρεις γραμμές.
Μπολζάνο στην
Ακριβώς αυτό είχα κατά νου. Ας συμπληρώσω για όφελος των μαθητών μας το αυτονόητο που λείπει: Υπάρχει
 με
με  . Παίρνω λοιπόν
. Παίρνω λοιπόν  . Τελειώσαμε.
. Τελειώσαμε.

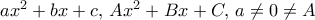 υπάρχει μία συνάρτηση
υπάρχει μία συνάρτηση  τέτοια ώστε για κάθε
τέτοια ώστε για κάθε  ισχύει
ισχύει 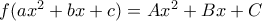 . Δείξτε ότι υπάρχουν πραγματικοί αριθμοί
. Δείξτε ότι υπάρχουν πραγματικοί αριθμοί  και διάστημα
και διάστημα  της μορφής
της μορφής ![(-\infty ,\, t] (-\infty ,\, t]](/forum/ext/geomar/texintegr/latexrender/pictures/df5b88014702886dea3656f321a7d9f2.png) ή της μορφής
ή της μορφής  , τέτοια ώστε
, τέτοια ώστε  για κάθε
για κάθε  .
. .
. του
του  για τις οποίες ισχύει
για τις οποίες ισχύει  . Π.χ. οι
. Π.χ. οι  είναι τέτοιες.
είναι τέτοιες.  παίρνει την ίδια τιμή (αυτό είναι αυτονόητο αφού το γράφημά της έχει σχήμα U). Τέτοιες π.χ. είναι οι
παίρνει την ίδια τιμή (αυτό είναι αυτονόητο αφού το γράφημά της έχει σχήμα U). Τέτοιες π.χ. είναι οι  , όπου η κοινή τιμή είναι
, όπου η κοινή τιμή είναι  .
.  και
και  .
.  .
.  έπεται
έπεται  (την περίπτωση
(την περίπτωση  θα την δούμε χωριστά). Άρα
θα την δούμε χωριστά). Άρα  .
. στο σύνολο τιμών της
στο σύνολο τιμών της  , όπως θέλαμε με
, όπως θέλαμε με 
 , θέτουμε
, θέτουμε  . Έπεται
. Έπεται  , oπότε
, oπότε  , και η δοθείσα γίνεται
, και η δοθείσα γίνεται  , και λοιπά, όπως πριν.
, και λοιπά, όπως πριν. οποιαδήποτε τιμή έξω από το σύνολο τιμών της
οποιαδήποτε τιμή έξω από το σύνολο τιμών της  .
. έτσι ώστε η εξίσωση
έτσι ώστε η εξίσωση 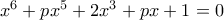 να έχει τουλάχιστον δύο (διαφορετικές) ρητές ρίζες.
να έχει τουλάχιστον δύο (διαφορετικές) ρητές ρίζες.  .
.

 . Παρατηρούμε ότι αν δώσουμε στο
. Παρατηρούμε ότι αν δώσουμε στο  , τότε το αντίστοιχο
, τότε το αντίστοιχο  ). Με άλλα λόγια βρήκαμε άπειρα το πλήθος ρητά
). Με άλλα λόγια βρήκαμε άπειρα το πλήθος ρητά  ριζα της εξίσωσης, τότε (εδώ είναι το κλειδί) και η
ριζα της εξίσωσης, τότε (εδώ είναι το κλειδί) και η  είναι ρίζα. Πράγματι
είναι ρίζα. Πράγματι  . Τελειώσαμε.
. Τελειώσαμε. δύο
δύο ![[P(x)] = [Q(x)] [P(x)] = [Q(x)]](/forum/ext/geomar/texintegr/latexrender/pictures/f43840616d6b82f3d2dc409a7dae2730.png) (το
(το ![[.] [.]](/forum/ext/geomar/texintegr/latexrender/pictures/d0b10a15db40a36d59fddb83ef024cf2.png) (συμβολίζει "ακέραιο μέρος"). Δείξτε ότι τα πολυώνυμα είναι ίσα.
(συμβολίζει "ακέραιο μέρος"). Δείξτε ότι τα πολυώνυμα είναι ίσα.  σε
σε ![[P(n)] = [Q(n)] [P(n)] = [Q(n)]](/forum/ext/geomar/texintegr/latexrender/pictures/61b0da4eaaf8e27252b412ea691e786a.png) (το
(το 
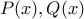 δεν είναι σταθερά αλλιώς πάλι έχουμε το αντιπαράδειγμα
δεν είναι σταθερά αλλιώς πάλι έχουμε το αντιπαράδειγμα  .
. είναι φραγμένο, άρα και σταθερό. Έστω
είναι φραγμένο, άρα και σταθερό. Έστω  όπου χωρίς βλάβη της γενικότητας
όπου χωρίς βλάβη της γενικότητας  . Αφού το
. Αφού το  είναι μη σταθερό, θα είναι επί σε κάποιο άπειρο διάστημα
είναι μη σταθερό, θα είναι επί σε κάποιο άπειρο διάστημα  ώστε
ώστε  για κάποιο
για κάποιο  . Αν
. Αν  , τότε από τη μία θα έχουμε
, τότε από τη μία θα έχουμε ![[Q(t)] < n [Q(t)] < n](/forum/ext/geomar/texintegr/latexrender/pictures/f70607a30ce496c5a5ab3320de051eb3.png) αλλά από την άλλη θα έχουμε
αλλά από την άλλη θα έχουμε ![[P(t)] = [Q(t)+c] = n [P(t)] = [Q(t)+c] = n](/forum/ext/geomar/texintegr/latexrender/pictures/fc62e17a76d7ebfb0e6d5eb1bf0ff413.png) , άτοπο. Άρα
, άτοπο. Άρα  και
και  για κάθε
για κάθε  .
. ισχύει
ισχύει ![[P(n)]=[Q(n)] [P(n)]=[Q(n)]](/forum/ext/geomar/texintegr/latexrender/pictures/596a1c45d3144bff5b8624b156253e96.png) . Σε αυτή την περίπτωση το συμπέρασμα είναι ότι τα
. Σε αυτή την περίπτωση το συμπέρασμα είναι ότι τα  διαφέρουν κατά σταθερά. Η λύση του Δημήτρη το δείχνει αυτό.
διαφέρουν κατά σταθερά. Η λύση του Δημήτρη το δείχνει αυτό.  για το οποίο ισχύει
για το οποίο ισχύει
 μας έκανε μια χαρά. Για να φτάσουμε σε πολυώνυμο
μας έκανε μια χαρά. Για να φτάσουμε σε πολυώνυμο  οστού βαθμού χωρίς να αλλάξουν οι τιμές που θέλουμε αρκεί να προσθέσουμε το
οστού βαθμού χωρίς να αλλάξουν οι τιμές που θέλουμε αρκεί να προσθέσουμε το  που είναι
που είναι  .
. είναι βαθμού
είναι βαθμού  . Άρα για κάποιο
. Άρα για κάποιο  είναι
είναι  . Και λοιπά.
. Και λοιπά. για κάποια επολογή των προσήμων. Αν
για κάποια επολογή των προσήμων. Αν  , να βρεθεί πολυώνυμο.
, να βρεθεί πολυώνυμο. (με δοκιμές)
(με δοκιμές) δοκιμές, όπως έκανες. Αν επιμένεις, τότε θα βάλω ένα πολυώνυμο βαθμού
δοκιμές, όπως έκανες. Αν επιμένεις, τότε θα βάλω ένα πολυώνυμο βαθμού  και άντε να δω πώς θα κάνεις τις
και άντε να δω πώς θα κάνεις τις  δοκιμές.
δοκιμές.