Έστω

το σύνολο όλων των αριθμών που μπορούν να προκύψουν με τον τερματισμό της διαδικασίας.
Έστω επίσης

το ζητούμενο μέγιστο του

.
Παρατηρώ ότι

τέτοια ώστε

και

.
Επίσης, αν
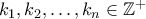
ικανοποιούν την

και επιπλέον

, τότε και κάθε μετάθεση
αυτής της

άδας ικανοποιεί τα παραπάνω.
Άρα, από την ανισότητα της αναδιάταξης για να βρούμε το

αρκεί να ελέγξουμε

άδες με

.
Θα δείξουμε ότι

.
Αρχικά, δείχνουμε ότι

. Διατάσσουμε στον πίνακα τους αριθμούς από τα αριστερά προς τα δεξιά
σε αύξουσα σειρά. Έπειτα σε κάθε βήμα αντικαθιστούμε τους δύο αριστερά αριθμούς με τον αριθμητικό μέσο τους, τον οποίο τοποθετούμε
αριστερά της υπόλοιπης λίστας.
Έτσι, στο τέλος θα μείνει ο αριθμός

.
Πάμε τώρα επαγωγικά να δείξουμε το ζητούμενο.
Για

έχουμε εύκολα ότι

, οπότε ελέγxουμε ότι

.
Έστω

ώστε

.
Θεωρούμε

,όπως πάνω.
Θα δείξουμε ότι
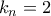
. Έστω προς άτοπο ότι

. Τότε και

.
Άρα:




, άτοπο.
Αφού τώρα
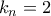
έχουμε ότι

όπου

.
Για να είναι λοιπόν το

μέγιστο πρέπει

,οπότε θα έχουμε

όπως θέλαμε.
 .
.  αριθμούς που είναι γραμμένοι στον πίνακα,
αριθμούς που είναι γραμμένοι στον πίνακα, 
 το σύνολο όλων των αριθμών που μπορούν να προκύψουν με τον τερματισμό της διαδικασίας.
το σύνολο όλων των αριθμών που μπορούν να προκύψουν με τον τερματισμό της διαδικασίας. το ζητούμενο μέγιστο του
το ζητούμενο μέγιστο του  .
. τέτοια ώστε
τέτοια ώστε 
 .
.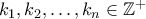 ικανοποιούν την
ικανοποιούν την  και επιπλέον
και επιπλέον  , τότε και κάθε μετάθεση
, τότε και κάθε μετάθεση  άδας ικανοποιεί τα παραπάνω.
άδας ικανοποιεί τα παραπάνω. .
. .
. . Διατάσσουμε στον πίνακα τους αριθμούς από τα αριστερά προς τα δεξιά
. Διατάσσουμε στον πίνακα τους αριθμούς από τα αριστερά προς τα δεξιά  .
. έχουμε εύκολα ότι
έχουμε εύκολα ότι  , οπότε ελέγxουμε ότι
, οπότε ελέγxουμε ότι  .
. ώστε
ώστε  .
. ,όπως πάνω.
,όπως πάνω.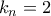 . Έστω προς άτοπο ότι
. Έστω προς άτοπο ότι  . Τότε και
. Τότε και  .
.


 , άτοπο.
, άτοπο. όπου
όπου  .
.  ,οπότε θα έχουμε
,οπότε θα έχουμε  όπως θέλαμε.
όπως θέλαμε.