 μεταξύ των ψηφίων του αριθμού
μεταξύ των ψηφίων του αριθμού  (
( άσοι) ώστε το τελικό αποτέλεσμα να είναι πολλαπλάσιο του
άσοι) ώστε το τελικό αποτέλεσμα να είναι πολλαπλάσιο του  ?
?Συντονιστές: Demetres, socrates, silouan
 μεταξύ των ψηφίων του αριθμού
μεταξύ των ψηφίων του αριθμού  (
( άσοι) ώστε το τελικό αποτέλεσμα να είναι πολλαπλάσιο του
άσοι) ώστε το τελικό αποτέλεσμα να είναι πολλαπλάσιο του  ?
?Πολλή ωραία ασκησούλα.
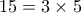 (πολλαπλάσιο του
(πολλαπλάσιο του  ), όπου και αν βάλουμε τα
), όπου και αν βάλουμε τα  , ο αριθμός που προκύπτει είναι πολλαπλάσιο του
, ο αριθμός που προκύπτει είναι πολλαπλάσιο του  (κριτήριο διαιρετότητας του
(κριτήριο διαιρετότητας του  ). Άρα πρέπει να μεριμνήσουμε ώστε ο αριθμός που προκύπτει να είναι πολλαπλάσιο του
). Άρα πρέπει να μεριμνήσουμε ώστε ο αριθμός που προκύπτει να είναι πολλαπλάσιο του  , που σημαίνει ότι το τελευταίο ψηφίο πρέπει να είναι
, που σημαίνει ότι το τελευταίο ψηφίο πρέπει να είναι  . Άρα πρέπει να έχουμε ακριβώς
. Άρα πρέπει να έχουμε ακριβώς  προσθετέους (ο καθένας λήγει σε
προσθετέους (ο καθένας λήγει σε  ) στην πρόσθεση. Δηλαδή να μπουν ακριβώς
) στην πρόσθεση. Δηλαδή να μπουν ακριβώς  "συν" στα
"συν" στα  κενά της παράστασης
κενά της παράστασης  (
( άσοι). Έχουμε δηλαδή
άσοι). Έχουμε δηλαδή  τρόπους.
τρόπους.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες