Σελίδα 1 από 1
Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 2:21 pm
από JimNt.
Παίρνουμε

σημεία πάνω σε έναν κύκλο, τα οποία ενώνουμε ανα

με ένα ευθύγραμμο τμήμα. (Έχουμε συνολικά

τέτοια τμήματα). Αν δίνεται ότι τα τμήματα αυτά ανα τρία δεν συντρέχουν στο εσωτερικό του κύκλου, να βρείτε το πλήθος των περιοχών στις οποίες χωρίζεται ο κύκλος από τα τμήματα αυτά. Για μαθητές.
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 3:38 pm
από harrisp
Είχα γράψει

ως απάντηση αλλα για 6 σημεία είναι λάθος!!!
Δείτε το !
Το πρόβλημα αποκτά τεράστιο ενδιαφέρον!
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 3:51 pm
από harrisp
Εχω βρει μια απάντηση που περιέχει τον τύπο του Euler αλλα δεν ειναι για τον φάκελο και ψάχνω και αλλη!
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 3:52 pm
από min##
Το λεγόμενο ''Moser's circle problem''
hint: v-e+f=2,handshake lemma
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 4:03 pm
από JimNt.
Δεν είχα το παραπάνω υπόψη μου... Λύνεται με πολύ πιο στοιχειώδη μέσα...
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τρί Απρ 18, 2017 9:20 pm
από Demetres
ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Είχα γράψει

ως απάντηση αλλα για 6 σημεία είναι λάθος!!!
Δείτε το !
Το πρόβλημα αποκτά τεράστιο ενδιαφέρον!
Από τα αγαπημένα μου προβλήματα ακριβώς για αυτόν τον λόγο. Η ακολουθία ξεκινάει ως εξής:

.
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Τετ Απρ 19, 2017 12:07 am
από Διονύσιος Αδαμόπουλος
Ο κύκλος ακόμα και χωρίς ευθύγραμμα τμήματα αποτελεί από μόνος του

περιοχή.
Έστω ότι υπάρχουν ήδη κάποια ευθύγραμμα τμήματα. Για κάθε επιπλέον ευθύγραμμο τμήμα που δημιουργείται μεταξύ

σημείων του κύκλου έχουμε τις εξής περιπτώσεις:
α) Αν το νέο τμήμα δεν τέμνεται από κανένα άλλο τμήμα τότε δημιουργεί μια επιπλέον περιοχή (χωρίζει μια προϋπάρχουσα περιοχή σε δύο περιοχές).
β) Αν το νέο τμήμα τέμνεται από

άλλα τμήματα, τότε αυτό χωρίζεται σε

μικρότερα τμήματα, δημιουργώντας

επιπλέον περιοχές.
Συγχωνεύοντας τις δύο περιπτώσεις σε μία, μπορούμε να πούμε ότι κάθε νέο τμήμα που τέμνεται σε

(με

) σημεία από άλλα τμήματα δημιουργεί

νέες περιοχές.
Δηλαδή έχουμε:
Πλήθος περιοχών

πλήθος ευθυγράμμων τμημάτων

πλήθος σημείων τομής

Βέβαια ο παραπάνω τύπος ισχύει αν

. Διαφορετικά:
Αν
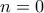
ή

τότε έχουμε

περιοχή.
Αν

ή

τότε έχουμε

περιοχές.
Υ.Γ.
Σε αυτό το σημείο αναρωτιέμαι αν τα παραπάνω αρκούν ή χρειάζεται κάποια "κανονική απόδειξη" π.χ. επαγωγή.
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Παρ Απρ 21, 2017 5:09 pm
από Διονύσιος Αδαμόπουλος
Διονύσιος Αδαμόπουλος έγραψε:
Βέβαια ο παραπάνω τύπος ισχύει αν

.
Κάπου είδα ότι θα μπορούσαμε να ορίσουμε ότι

αν

. Αν ισχύει αυτό, τότε ο αρχικός τύπος θα ισχύει για όλα τα

.
Διονύσιος Αδαμόπουλος έγραψε:
Υ.Γ.
Σε αυτό το σημείο αναρωτιέμαι αν τα παραπάνω αρκούν ή χρειάζεται κάποια "κανονική απόδειξη" π.χ. επαγωγή.
Σε αυτό δεν απάντησε κανείς...

Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Παρ Απρ 21, 2017 5:22 pm
από cretanman
Για τον ίδιο λόγο που αναφέρει ο Δημήτρης είναι και για μένα ένα από τα αγαπημένα προβλήματα. Φαίνεται να ακολουθείται ένα μοτίβο το οποίο κάποια στιγμή (με 6 σημεία) χαλάει...
Είχε συζητηθεί
εδώ και ήταν θέμα στον Αρχιμήδη το 1999 στο οποίο είχα συμμετάσχει ως μαθητής (τα θέματα
εδώ).
Αλέξανδρος
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Παρ Απρ 21, 2017 9:48 pm
από Διονύσιος Αδαμόπουλος
Διονύσιος Αδαμόπουλος έγραψε:
Βέβαια ο παραπάνω τύπος ισχύει αν

.
Κάπου είδα ότι θα μπορούσαμε να ορίσουμε ότι

αν

. Ισχύει πράγματι;
Αν ισχύει αυτό, τότε ο αρχικός τύπος θα ισχύει για όλα τα

.
Διονύσιος Αδαμόπουλος έγραψε:
Υ.Γ.
Σε αυτό το σημείο αναρωτιέμαι αν τα παραπάνω αρκούν ή χρειάζεται κάποια "κανονική απόδειξη" π.χ. επαγωγή.
Σε αυτό δεν απάντησε κανείς...
 Ας βάλουμε και ένα πρόσθετο ερώτημα:
Ας βάλουμε και ένα πρόσθετο ερώτημα:
β) Ποιο είναι το πλήθος των ευθυγράμμων τμημάτων στα οποία χωρίζονται αυτές οι

χορδές μέσω των σημείων τομής τους.
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Παρ Απρ 21, 2017 11:08 pm
από min##
Από τον τύπο V-E+F=2 όπου στο V προσμετρούνται τα σημεία τομής των χορδών (

) και τα n σημεία, στο F προσμετράται η περιοχή εκτός του κύκλου και στο e τα καμπυλόγραμμα τμήματα μεταξύ δύο διαδοχικών σημείων(n στο πλήθος),παίρνουμε

+n-(πλήθοςζητούμενωντμημάτων +n)+

+

=0.Λύνοντας ως προς το πλήθος των ζητούμενων τμημάτων(έστω e') παίρνουμε e'=2

+

.Τέλος αφαιρούμε τα n μη τεμνόμενα τμήματα και παίρνουμε: e'=2

+

-n..
Re: Από Αναδρομική σε Αναδρομική!
Δημοσιεύτηκε: Κυρ Απρ 30, 2017 10:52 pm
από Διονύσιος Αδαμόπουλος
Διονύσιος Αδαμόπουλος έγραψε:
Ας βάλουμε και ένα πρόσθετο ερώτημα:
β) Ποιο είναι το πλήθος των ευθυγράμμων τμημάτων στα οποία χωρίζονται αυτές οι

χορδές μέσω των σημείων τομής τους.
min## έγραψε:Από τον τύπο V-E+F=2 όπου στο V προσμετρούνται τα σημεία τομής των χορδών (

) και τα n σημεία, στο F προσμετράται η περιοχή εκτός του κύκλου και στο e τα καμπυλόγραμμα τμήματα μεταξύ δύο διαδοχικών σημείων(n στο πλήθος),παίρνουμε

+n-(πλήθοςζητούμενωντμημάτων +n)+

+

=0.Λύνοντας ως προς το πλήθος των ζητούμενων τμημάτων(έστω e') παίρνουμε e'=2

+

.Τέλος αφαιρούμε τα n μη τεμνόμενα τμήματα και παίρνουμε: e'=2

+

-n..
Νομίζω πως δεν υπάρχει λόγος να αφαιρέσουμε τα

μη τεμνόμενα τμήματα, όπως λες στο τέλος της λύσης σου.
Εναλλακτικά:
Κάθε χορδή από μόνη της αποτελεί ένα ευθύγραμμο τμήμα. Κάθε σημείο τομής που βρίσκεται πάνω σε μια χορδή δημιουργεί ένα επιπλέον τμήμα σε αυτή τη χορδή (π.χ. αν μια χορδή περιέχει

σημεία τομής τότε χωρίζεται σε

τμήματα).
Όμως κάθε σημείο τομής βρίσκεται σε

χορδές. Επομένως έχουμε:
Πλήθος τμημάτων

πλήθος χορδών

πλήθος σημείων τομής

 σημεία πάνω σε έναν κύκλο, τα οποία ενώνουμε ανα
σημεία πάνω σε έναν κύκλο, τα οποία ενώνουμε ανα  με ένα ευθύγραμμο τμήμα. (Έχουμε συνολικά
με ένα ευθύγραμμο τμήμα. (Έχουμε συνολικά  τέτοια τμήματα). Αν δίνεται ότι τα τμήματα αυτά ανα τρία δεν συντρέχουν στο εσωτερικό του κύκλου, να βρείτε το πλήθος των περιοχών στις οποίες χωρίζεται ο κύκλος από τα τμήματα αυτά. Για μαθητές.
τέτοια τμήματα). Αν δίνεται ότι τα τμήματα αυτά ανα τρία δεν συντρέχουν στο εσωτερικό του κύκλου, να βρείτε το πλήθος των περιοχών στις οποίες χωρίζεται ο κύκλος από τα τμήματα αυτά. Για μαθητές. σημεία πάνω σε έναν κύκλο, τα οποία ενώνουμε ανα
σημεία πάνω σε έναν κύκλο, τα οποία ενώνουμε ανα  με ένα ευθύγραμμο τμήμα. (Έχουμε συνολικά
με ένα ευθύγραμμο τμήμα. (Έχουμε συνολικά  τέτοια τμήματα). Αν δίνεται ότι τα τμήματα αυτά ανα τρία δεν συντρέχουν στο εσωτερικό του κύκλου, να βρείτε το πλήθος των περιοχών στις οποίες χωρίζεται ο κύκλος από τα τμήματα αυτά. Για μαθητές.
τέτοια τμήματα). Αν δίνεται ότι τα τμήματα αυτά ανα τρία δεν συντρέχουν στο εσωτερικό του κύκλου, να βρείτε το πλήθος των περιοχών στις οποίες χωρίζεται ο κύκλος από τα τμήματα αυτά. Για μαθητές. ως απάντηση αλλα για 6 σημεία είναι λάθος!!!
ως απάντηση αλλα για 6 σημεία είναι λάθος!!! .
. περιοχή.
περιοχή. άλλα τμήματα, τότε αυτό χωρίζεται σε
άλλα τμήματα, τότε αυτό χωρίζεται σε  μικρότερα τμήματα, δημιουργώντας
μικρότερα τμήματα, δημιουργώντας  ) σημεία από άλλα τμήματα δημιουργεί
) σημεία από άλλα τμήματα δημιουργεί  πλήθος ευθυγράμμων τμημάτων
πλήθος ευθυγράμμων τμημάτων  πλήθος σημείων τομής
πλήθος σημείων τομής 
 . Διαφορετικά:
. Διαφορετικά: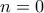 ή
ή  τότε έχουμε
τότε έχουμε  περιοχή.
περιοχή. ή
ή  τότε έχουμε
τότε έχουμε  περιοχές.
περιοχές. αν
αν  . Αν ισχύει αυτό, τότε ο αρχικός τύπος θα ισχύει για όλα τα
. Αν ισχύει αυτό, τότε ο αρχικός τύπος θα ισχύει για όλα τα  χορδές μέσω των σημείων τομής τους.
χορδές μέσω των σημείων τομής τους. ) και τα n σημεία, στο F προσμετράται η περιοχή εκτός του κύκλου και στο e τα καμπυλόγραμμα τμήματα μεταξύ δύο διαδοχικών σημείων(n στο πλήθος),παίρνουμε
) και τα n σημεία, στο F προσμετράται η περιοχή εκτός του κύκλου και στο e τα καμπυλόγραμμα τμήματα μεταξύ δύο διαδοχικών σημείων(n στο πλήθος),παίρνουμε  πλήθος χορδών
πλήθος χορδών  πλήθος σημείων τομής
πλήθος σημείων τομής 