 και
και 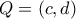 του επιπέδου
του επιπέδου  όπου
όπου  ακέραιοι με
ακέραιοι με  Θέλουμε να μεταβούμε από το σημείο
Θέλουμε να μεταβούμε από το σημείο  στο σημείο
στο σημείο  κινούμενοι σε κάθε βήμα κατά
κινούμενοι σε κάθε βήμα κατά  είτε δεξιά είτε πάνω. Με πόσους τρόπους μπορεί να γίνει αυτό αν δεν επιτρέπεται να αγγίξουμε την ευθεία
είτε δεξιά είτε πάνω. Με πόσους τρόπους μπορεί να γίνει αυτό αν δεν επιτρέπεται να αγγίξουμε την ευθεία 
Συντονιστές: Demetres, socrates, silouan
 και
και 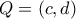 του επιπέδου
του επιπέδου  όπου
όπου  ακέραιοι με
ακέραιοι με  Θέλουμε να μεταβούμε από το σημείο
Θέλουμε να μεταβούμε από το σημείο  στο σημείο
στο σημείο  κινούμενοι σε κάθε βήμα κατά
κινούμενοι σε κάθε βήμα κατά  είτε δεξιά είτε πάνω. Με πόσους τρόπους μπορεί να γίνει αυτό αν δεν επιτρέπεται να αγγίξουμε την ευθεία
είτε δεξιά είτε πάνω. Με πόσους τρόπους μπορεί να γίνει αυτό αν δεν επιτρέπεται να αγγίξουμε την ευθεία 
Ενδεχομένως να έχω λάθος αλλά κάνω μία προσπάθεια :
 οι τρόποι.
οι τρόποι.
 δηλώνει το ύψος ενώ το
δηλώνει το ύψος ενώ το  το πόσο δεξιά είναι και γράφουμε
το πόσο δεξιά είναι και γράφουμε  π.χ το σημείο
π.χ το σημείο  είναι το
είναι το  και ας πούμε
και ας πούμε  τον αριθμό των τρόπων με τους οποίους μπορούμε να φτάσουμε στο
τον αριθμό των τρόπων με τους οποίους μπορούμε να φτάσουμε στο  .Σε κάθε σημείο είναι
.Σε κάθε σημείο είναι  (βλέπε Αρχιμήδης Juniors 2009 θέμα 4).
(βλέπε Αρχιμήδης Juniors 2009 θέμα 4).






Σας ευχαριστώ πολύ! Δεν ήξερα πως είναι τόσο γνωστό, βρήκα στο Wikipedia και αυτόν τον τύποΛάμπρος Κατσάπας έγραψε: ↑Κυρ Μαρ 24, 2019 1:59 pmΓεια σου Πρόδρομε. Για ρίξε μια ματιά Bertrand's ballot theorem, πρόβλημα ψηφοφορίας στη θεωρία πιθανοτήτων, αρχή ανακλάσης - τυχαίος περίπατος. Θα βρεις βρεις ενδιαφέροντα και ωραία πράγματα. Το παραπάνω πρόβλημα είναι αρκετά γνωστό.

 ο οποίος είναι ισοδύναμος αυτού που βρήκα στην λύση μου αφού:
ο οποίος είναι ισοδύναμος αυτού που βρήκα στην λύση μου αφού:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης