Καλοί Αριθμοί
Συντονιστές: cretanman, silouan, rek2
Καλοί Αριθμοί
Καλησπέρα σε όλους. Ορίστε μία άσκηση που κατασκεύασα:
Ένας θετικός ακέραιους λέγεται <<καλός>>, εάν όλα του τα ψηφία (τουλάχιστον δύο στο πλήθος) είναι ίσα μεταξύ τους. Είναι άραγε δυνατόν κάποιος καλός αριθμός να είναι τέλειο τετράγωνο ακεραίου;
Ένας θετικός ακέραιους λέγεται <<καλός>>, εάν όλα του τα ψηφία (τουλάχιστον δύο στο πλήθος) είναι ίσα μεταξύ τους. Είναι άραγε δυνατόν κάποιος καλός αριθμός να είναι τέλειο τετράγωνο ακεραίου;
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Καλοί Αριθμοί
Aπάντηση: Οι αριθμοί
 (τουλάχιστον δύο επαναλήψεις του ψηφίου
(τουλάχιστον δύο επαναλήψεις του ψηφίου  ) δεν μπορεί να είναι τέλεια τετράγωνα.
) δεν μπορεί να είναι τέλεια τετράγωνα.Πράγματι, αποκλείονται οι περιπτώσεις
 γιατί κανένα τέλειο τετράγωνο δεν λήγει σε αυτούς. (Tα τέλεια τετράγωνα λήγουν σε
γιατί κανένα τέλειο τετράγωνο δεν λήγει σε αυτούς. (Tα τέλεια τετράγωνα λήγουν σε  , και λοιπά.)
, και λοιπά.) Για
 , μία ισότητα της μορφής
, μία ισότητα της μορφής  δίνει
δίνει  άρτιος,
άρτιος,  , οπότε
, οπότε  . To οποίο όμως θα δούμε παρακάτω (τελευταίες δύο γραμμές) ότι δεν γίνεται.
. To οποίο όμως θα δούμε παρακάτω (τελευταίες δύο γραμμές) ότι δεν γίνεται. Για
 , μία ισότητα της μορφής
, μία ισότητα της μορφής  δίνει
δίνει  πολλαπλάσιο του
πολλαπλάσιο του  ,
,  , οπότε
, οπότε  . Άτοπο αφού το ένα μέλος είναι πολλαπλάσιο του
. Άτοπο αφού το ένα μέλος είναι πολλαπλάσιο του  και το άλλο δεν είναι.
και το άλλο δεν είναι. Για
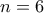 , μία ισότητα της μορφής
, μία ισότητα της μορφής  δίνει
δίνει  άρτιος,
άρτιος,  , οπότε
, οπότε  . Άτοπο αφού το ένα μέλος είναι περιττό και το άλλο άρτιος.
. Άτοπο αφού το ένα μέλος είναι περιττό και το άλλο άρτιος. Μένουν οι περιπτώσεις
 και
και  . Είναι
. Είναι  και
και  , οπότε και οι δύο είναι
, οπότε και οι δύο είναι  . Άρα δεν είναι τέλεια τετράγωνα γιατί αυτά είναι ισότιμα με
. Άρα δεν είναι τέλεια τετράγωνα γιατί αυτά είναι ισότιμα με  ή
ή 
 .
.Edit: Διόρθωσα μικρή αβλεψία (βλέπε σχόλιο του θεματοθέτη Joaakim στο επόμενο ποστ). Τον ευχαριστώ.
τελευταία επεξεργασία από Mihalis_Lambrou σε Τρί Αύγ 03, 2021 8:02 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Καλοί Αριθμοί
Ωραία λύση, γραμμένη ώστε να γίνεται κατανοητή από όλους.
 , το οποίο μπορεί όμως να διορθωθεί.
, το οποίο μπορεί όμως να διορθωθεί.
Ένας τρόπος είναι με , αφού δίνει
, αφού δίνει  , άτοπο, αφού το
, άτοπο, αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
.
Η δική μου λύση στηρίζεται στην χρήση ισοτιμιών . Θα δω μήπως την ανεβάσω αύριο.
. Θα δω μήπως την ανεβάσω αύριο.
Έχετε όμως ένα λαθάκι σε αυτό το σημείο- πρέπει να είναιMihalis_Lambrou έγραψε: ↑Τρί Αύγ 03, 2021 6:43 pm
Για, μία ισότητα της μορφής
δίνει
άρτιος,
, οπότε
. Άτοπο αφού το ένα μέλος είναι περιττό και το άλλο άρτιος.
 , το οποίο μπορεί όμως να διορθωθεί.
, το οποίο μπορεί όμως να διορθωθεί.Ένας τρόπος είναι με
 , αφού δίνει
, αφού δίνει  , άτοπο, αφού το
, άτοπο, αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
.Η δική μου λύση στηρίζεται στην χρήση ισοτιμιών
 . Θα δω μήπως την ανεβάσω αύριο.
. Θα δω μήπως την ανεβάσω αύριο.-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Καλοί Αριθμοί
Σωστά. Απροσεξία μου. Τώρα το διόρθωσα στο αρχικό μου ποστ.Joaakim έγραψε: ↑Τρί Αύγ 03, 2021 7:44 pmΩραία λύση, γραμμένη ώστε να γίνεται κατανοητή από όλους.
Έχετε όμως ένα λαθάκι σε αυτό το σημείο- πρέπει να είναιMihalis_Lambrou έγραψε: ↑Τρί Αύγ 03, 2021 6:43 pm
Για, μία ισότητα της μορφής
δίνει
άρτιος,
, οπότε
. Άτοπο αφού το ένα μέλος είναι περιττό και το άλλο άρτιος.
, το οποίο μπορεί όμως να διορθωθεί.
ΕΥΧΑΡΙΣΤΩ.
- Lymperis Karras
- Δημοσιεύσεις: 170
- Εγγραφή: Παρ Νοέμ 06, 2020 5:16 pm
Re: Καλοί Αριθμοί
Ας το δούμε και με  .
.
Καταρχάς η εξίσωση γράφεται . Όπου
. Όπου  το ψηφίο και
το ψηφίο και  ο αριθμός των ψηφίων.
ο αριθμός των ψηφίων.
Με παίρνω
παίρνω 
Άρα μένει να εξετάσω τις περιπτώσεις
Αποκλείουμε τις περιπτώσεις για τον ίδιο λόγο που ανέφερε ο κ. Λάμπρου.
για τον ίδιο λόγο που ανέφερε ο κ. Λάμπρου.
Εναλλακτικά δουλεύουμε ως εξής:
Για έχω
έχω  .
.
Με παίρνω
παίρνω  , άτοπο.
, άτοπο.
Για με
με  άτοπο πάλι.
άτοπο πάλι.
Για έχω
έχω  .
.
Τώρα είναι . Με
. Με  έχω
έχω  , άτοπο.
, άτοπο.
Μένει η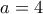 .
.
Για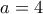 έχω
έχω  .
.
Άρα .
.
Με έχω όμως ότι
έχω όμως ότι  , άτοπο.
, άτοπο.
Και λοιπά.
 .
.Καταρχάς η εξίσωση γράφεται
 . Όπου
. Όπου  το ψηφίο και
το ψηφίο και  ο αριθμός των ψηφίων.
ο αριθμός των ψηφίων.Με
 παίρνω
παίρνω 
Άρα μένει να εξετάσω τις περιπτώσεις

Αποκλείουμε τις περιπτώσεις
 για τον ίδιο λόγο που ανέφερε ο κ. Λάμπρου.
για τον ίδιο λόγο που ανέφερε ο κ. Λάμπρου.Εναλλακτικά δουλεύουμε ως εξής:
Για
 έχω
έχω  .
. Με
 παίρνω
παίρνω  , άτοπο.
, άτοπο.Για
 με
με  άτοπο πάλι.
άτοπο πάλι.Για
 έχω
έχω  .
.Τώρα είναι
 . Με
. Με  έχω
έχω  , άτοπο.
, άτοπο.Μένει η
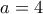 .
.Για
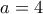 έχω
έχω  .
.Άρα
 .
.Με
 έχω όμως ότι
έχω όμως ότι  , άτοπο.
, άτοπο.Και λοιπά.
Ένας μαθηματικός χρειάζεται μολύβι, γόμα και μεγάλο καλάθι αχρήστων.
-Hilbert
-Hilbert
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Καλοί Αριθμοί
Μια προσπάθεια για σύντομη λύση.
Γράφουμε τον αριθμό ως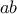 όπου
όπου  και
και  . Επειδή
. Επειδή  , αν τον γράψουμε σε γινόμενο πρώτων παραγόντων, θα έχει κάποιον πρώτο παράγοντα
, αν τον γράψουμε σε γινόμενο πρώτων παραγόντων, θα έχει κάποιον πρώτο παράγοντα  με
με  και
και  περιττό. Για να είναι ο
περιττό. Για να είναι ο 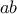 τέλειο τετράγωνο, πρέπει
τέλειο τετράγωνο, πρέπει  και άρα
και άρα  ή
ή  . Τότε όμως
. Τότε όμως  και άρα δεν είναι τέλειο τετράγωνο.
και άρα δεν είναι τέλειο τετράγωνο.
Γράφουμε τον αριθμό ως
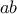 όπου
όπου  και
και  . Επειδή
. Επειδή  , αν τον γράψουμε σε γινόμενο πρώτων παραγόντων, θα έχει κάποιον πρώτο παράγοντα
, αν τον γράψουμε σε γινόμενο πρώτων παραγόντων, θα έχει κάποιον πρώτο παράγοντα  με
με  και
και  περιττό. Για να είναι ο
περιττό. Για να είναι ο 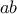 τέλειο τετράγωνο, πρέπει
τέλειο τετράγωνο, πρέπει  και άρα
και άρα  ή
ή  . Τότε όμως
. Τότε όμως  και άρα δεν είναι τέλειο τετράγωνο.
και άρα δεν είναι τέλειο τετράγωνο.Re: Καλοί Αριθμοί
Ένας θετικός ακέραιους  ψηφίων (
ψηφίων (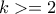 )λέγεται <<καλός>>, εάν τουλάχιστον
)λέγεται <<καλός>>, εάν τουλάχιστον  ψηφία είναι ίδια.Να βρεθούν όλοι οι καλοί αριθμοί που είναι τέλειο τετράγωνα.
ψηφία είναι ίδια.Να βρεθούν όλοι οι καλοί αριθμοί που είναι τέλειο τετράγωνα.
 problem
problem
 ψηφίων (
ψηφίων (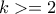 )λέγεται <<καλός>>, εάν τουλάχιστον
)λέγεται <<καλός>>, εάν τουλάχιστον  ψηφία είναι ίδια.Να βρεθούν όλοι οι καλοί αριθμοί που είναι τέλειο τετράγωνα.
ψηφία είναι ίδια.Να βρεθούν όλοι οι καλοί αριθμοί που είναι τέλειο τετράγωνα. problem
problem-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Καλοί Αριθμοί
Ενδιαφέρον. Δεν το γνώριζα αλλά ψάχνοντας στο ίντερνετ το όνομα που δίνεις, Oblath's problem, βρήκα ένα άρθρο των Ρουμάνων Gica και Panaiotopol εδώ με πλήρη λύση του προβλήματος.
Συγκεκριμένα, οι "μικρές" λύσεις είναι μόνο οι παρακάτω (αντιγράφω για χάρη του φόρουμ):
α) όλα τα οι διψήφια τέλεια τετράγωνα

β) οι τριψήφιοι

γ) ο τετραψήφιος

δ) οι πενταψήφιοι

Aπό εκεί και πέρα μόνο οι αριθμοί της μορφής
 .
.Ευχαριστούμε που μας άνοιξες το μονοπάτι.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
