 και πρώτη
και πρώτη  με
με  και:
και:
Συντονιστές: cretanman, silouan, rek2
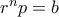 . Η εξίσωση γράφεται
. Η εξίσωση γράφεται 
 και ΜΚΔ
και ΜΚΔ πρέπει όλοι οι διαιρέτες του
πρέπει όλοι οι διαιρέτες του  να γράφονται στη μορφή αθροίσματος δύο τέλειων τετραγώνων (2). Άρα , από το θεώρημα του Fermat, οι περιττοί πρώτοι διαιρέτες, εφόσον υπάρχουν, είναι ίσοι με 1 modulo 4. Άρα
να γράφονται στη μορφή αθροίσματος δύο τέλειων τετραγώνων (2). Άρα , από το θεώρημα του Fermat, οι περιττοί πρώτοι διαιρέτες, εφόσον υπάρχουν, είναι ίσοι με 1 modulo 4. Άρα 
Μπορούμε να χρησιμοποιούμε και το εξής Λήμμα:
 είναι ακέραιοι με
είναι ακέραιοι με  πρώτο και
πρώτο και  , τότε
, τότε  και
και  .
. διαιρεί έναν εκ των
διαιρεί έναν εκ των  , τότε θα διαιρεί και τον άλλο, και αφού
, τότε θα διαιρεί και τον άλλο, και αφού  πρώτος, τότε
πρώτος, τότε  και
και  .
. δεν διαιρεί κανέναν εκ των
δεν διαιρεί κανέναν εκ των 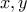 . Τότε
. Τότε  .
.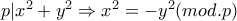 .
. , για φυσικό αριθμό
, για φυσικό αριθμό  .
. παίρνουμε:
παίρνουμε:
 , άτοπο.
, άτοπο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες