Να βρεθούν όλοι οι άρρητοι αριθμοί
 τέτοιοι ώστε οι
τέτοιοι ώστε οι  και
και  να είναι και οι δύο φυσικοί αριθμοί.
να είναι και οι δύο φυσικοί αριθμοί.Συντονιστές: cretanman, silouan, rek2
 τέτοιοι ώστε οι
τέτοιοι ώστε οι  και
και  να είναι και οι δύο φυσικοί αριθμοί.
να είναι και οι δύο φυσικοί αριθμοί.Eπαναφορά.Mihalis_Lambrou έγραψε: ↑Τρί Αύγ 03, 2021 8:57 pmΜικρή αλλαγή σκηνικού στην ίδια θεματολογία:
Να βρεθούν όλοι οι άρρητοι αριθμοίτέτοιοι ώστε οι
και
να είναι και οι δύο φυσικοί αριθμοί.
 και
και  . Τότε
. Τότε
 και αφού
και αφού  άρρητος συμπεραίνουμε ότι
άρρητος συμπεραίνουμε ότι  και
και  . Αν
. Αν  τότε η
τότε η  δίνει
δίνει  . Και οι δύο απαντήσεις είναι άρρητοι και ικανοποιούν και την
. Και οι δύο απαντήσεις είναι άρρητοι και ικανοποιούν και την  αφού τότε
αφού τότε 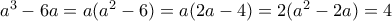 .
.Kαι άλλη μια λύση/παραλλαγή στο ίδιο μήκος κύματος.Mihalis_Lambrou έγραψε: ↑Τρί Αύγ 03, 2021 8:57 pmΜικρή αλλαγή σκηνικού στην ίδια θεματολογία:
Να βρεθούν όλοι οι άρρητοι αριθμοίτέτοιοι ώστε οι
και
να είναι και οι δύο φυσικοί αριθμοί.
 . Άρα
. Άρα  με
με  άρρηρτο. Oπότε
άρρηρτο. Oπότε  . Για να είναι ακέραιος πρέπει ο συντελεστής του (άρρητου)
. Για να είναι ακέραιος πρέπει ο συντελεστής του (άρρητου)  να είναι
να είναι  , οπότε
, οπότε  . Και λοιπά.
. Και λοιπά.Για να δούμε μια πιο ''μεθοδολογική'' αντιμετώπιση.Mihalis_Lambrou έγραψε: ↑Τρί Αύγ 03, 2021 8:57 pmΜικρή αλλαγή σκηνικού στην ίδια θεματολογία:
Να βρεθούν όλοι οι άρρητοι αριθμοίτέτοιοι ώστε οι
και
να είναι και οι δύο φυσικοί αριθμοί.
 με το
με το  δευτέρου βαθμού.
δευτέρου βαθμού. αρρητος ώστε τα
αρρητος ώστε τα  να είναι ακέραιοι.
να είναι ακέραιοι. με το
με το 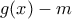 το υπόλοιπο θα είναι το πολυ πρώτου βαθμού.
το υπόλοιπο θα είναι το πολυ πρώτου βαθμού. οπότε και το
οπότε και το 
 o αριθμός
o αριθμός  είναι άρρητος.
είναι άρρητος.Θα δείξουμε ότι ο δεδομένος αριθμός είναι άρρητος. Έστω προς άτοπο ότι είναι ρητός.
 .
. είναι επίσης φυσικός.
είναι επίσης φυσικός. έχουμε
έχουμε  , άτοπο, αφού το
, άτοπο, αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  ,
, Ας τη δυσκολέψουμε λίγο:Mihalis_Lambrou έγραψε: ↑Πέμ Σεπ 02, 2021 10:37 amΣτην ίδια θεματολογία αλλά η λύση θέλει διαφορετικό επιχείρημα. Το εν λόγω επιχείρημα είναι απλό και γνωστό σε όσους έχουν ασχοληθεί με τέτοια θέματα, αλλά αναρτώ την άσκηση (για χάρη πληρότητας και) για να δουν το επιχείρημα όσοι ίσως δεν το γνωρίζουν.
Δίξτε ότι για κάθεo αριθμός
είναι άρρητος.
 o αριθμός
o αριθμός  είναι άρρητος.
είναι άρρητος.Η ωραία αυτή άσκηση, ξεχάστηκε. Ομολογώ ότι την ξεκίνησα με μόντουλα, όπως στην αρχική εκδοχή της, και δεν έβγαλα άκρη. Άρα τώρα αλλαγή πλεύσης.
 είναι άρρητος, ισοδύναμα ότι ο
είναι άρρητος, ισοδύναμα ότι ο  δεν είναι τέλειο τετράγωνο. Μας δολεύει να βάλουμε
δεν είναι τέλειο τετράγωνο. Μας δολεύει να βάλουμε  στην θέση του
στην θέση του  , και να ασχοληθούμε (ισοδύναμα) με τον αριθμό
, και να ασχοληθούμε (ισοδύναμα) με τον αριθμό 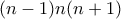 .
. 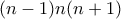 είναι τέλειο τετράγωνο, δηλαδή η ανάλυσή του σε πρώτους παράγοντες έχει όλους τους όρους σε άρτια δύναμη. Έστω
είναι τέλειο τετράγωνο, δηλαδή η ανάλυσή του σε πρώτους παράγοντες έχει όλους τους όρους σε άρτια δύναμη. Έστω  πρώτος παράγοντας του
πρώτος παράγοντας του  . Τότε αποκλείται να είναι πρώτος παράγοντας στην ανάλυση των
. Τότε αποκλείται να είναι πρώτος παράγοντας στην ανάλυση των  και
και  (άμεσο). Άρα ο
(άμεσο). Άρα ο  εμφανίζεται μόνο στον
εμφανίζεται μόνο στον  και άρα είναι σε άρτια δύναμη εκεί. Έπεται ότι από μόνος του ο
και άρα είναι σε άρτια δύναμη εκεί. Έπεται ότι από μόνος του ο  είναι τέλειο τετράγωνο. Έπεται ότι πρώτοι στην ανάλυση του γινομένου
είναι τέλειο τετράγωνο. Έπεται ότι πρώτοι στην ανάλυση του γινομένου  (δηλαδή όλοι οι υπόλοιποι) είναι επίσης σε άρτια δύναμη, οπότε ο
(δηλαδή όλοι οι υπόλοιποι) είναι επίσης σε άρτια δύναμη, οπότε ο 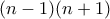 είναι και αυτός τέλειο τετράγωνο. Αλλά αυτό ειναι άτοπο γιατί ισούται με
είναι και αυτός τέλειο τετράγωνο. Αλλά αυτό ειναι άτοπο γιατί ισούται με  , που προφανώς δεν είναι τέλειο τετράγωνο (είναι ανάμεσα στα διαδοχικά
, που προφανώς δεν είναι τέλειο τετράγωνο (είναι ανάμεσα στα διαδοχικά  και
και  ). Τελειώσαμε.
). Τελειώσαμε.  στην θέση του
στην θέση του  , δηλαδή ο αριθμός μας είναι ο
, δηλαδή ο αριθμός μας είναι ο  (νέο
(νέο  ).
). (που τώρα δεν μπορεί να είναι ο
(που τώρα δεν μπορεί να είναι ο  ) λειτουργεί ατόφια. Μένει η περίπτωση όπου ο
) λειτουργεί ατόφια. Μένει η περίπτωση όπου ο  είναι άρτιος,
είναι άρτιος,  όπου
όπου  περιττός. Έστω ότι ο
περιττός. Έστω ότι ο  είναι τέλειο τετράγωνο. Όπως πριν κάθε (περιττός) πρώτος παράγοντας του
είναι τέλειο τετράγωνο. Όπως πριν κάθε (περιττός) πρώτος παράγοντας του  , που φυσικά δεν μπορεί να είναι παράγοντας των
, που φυσικά δεν μπορεί να είναι παράγοντας των  (άμεσο) πρέπει να είναι σε άρτια δύναμη. Άρα
(άμεσο) πρέπει να είναι σε άρτια δύναμη. Άρα  τέλειο τετράγωνο, οπότε και το γινόμενο
τέλειο τετράγωνο, οπότε και το γινόμενο  θα είναι τέλειο τετράγωνο (περιέχει όλους τους υπόλοιπους πρώτους παράγοντες σε άρτια δύναμη). Άτοπο.
θα είναι τέλειο τετράγωνο (περιέχει όλους τους υπόλοιπους πρώτους παράγοντες σε άρτια δύναμη). Άτοπο. ανά δύο δεν μπορούν να έχουν κοινό περιττό πρώτο παράγοντα. (Π.χ. αν ο
ανά δύο δεν μπορούν να έχουν κοινό περιττό πρώτο παράγοντα. (Π.χ. αν ο  διαιρεί τους
διαιρεί τους  και
και  τότε διαιρεί και το
τότε διαιρεί και το  επομένως
επομένως  .)
.)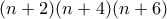 τέλειο τετράγωνο πρέπει κάθε ένας από τους
τέλειο τετράγωνο πρέπει κάθε ένας από τους  να είναι της μορφής
να είναι της μορφής  . Διαφορετικά κάθε ένας από αυτούς είτε θα είναι τέλειο τετράγωνο είτε το διπλάσιο ενός τέλειου τετραγώνου.
. Διαφορετικά κάθε ένας από αυτούς είτε θα είναι τέλειο τετράγωνο είτε το διπλάσιο ενός τέλειου τετραγώνου. 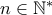 o αριθμός
o αριθμός  είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειο τετράγωνο.
είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειο τετράγωνο.Λήμμα: Το γινόμενο τεσσάρων διαδοχικών ακεραίων αυξημένο κατάMihalis_Lambrou έγραψε: ↑Παρ Σεπ 17, 2021 7:40 pm
Δίξτε ότι για κάθεo αριθμός
είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειο τετράγωνο.
 είναι τέλειο τετράγωνο ακεραίου.
είναι τέλειο τετράγωνο ακεραίου.
 .
.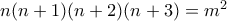 , με
, με  θετικό ακέραιο.
θετικό ακέραιο.  , άρα
, άρα  που εύκολα δίνει
που εύκολα δίνει 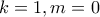 , άτοπο.
, άτοπο.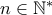 o αριθμός
o αριθμός ![\sqrt [3] {n(n+1)(n+2)} \sqrt [3] {n(n+1)(n+2)}](/forum/ext/geomar/texintegr/latexrender/pictures/28064768212fb5c9f37d5388eb8b9d1b.png) είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειος κύβος.
είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειος κύβος.Mihalis_Lambrou έγραψε: ↑Σάβ Σεπ 18, 2021 12:45 amΔίξτε ότι για κάθεo αριθμός
είναι άρρητος. Με άλλα λόγια δείξτε ότι η υπόριζη ποσότητα δεν είναι ποτέ τέλειος κύβος.
 αλλά
αλλά 
 δεν είναι ποτέ τέλειος κύβος.
δεν είναι ποτέ τέλειος κύβος. , ο αριθμός είναι
, ο αριθμός είναι  , και άρα προκύπτουν οι άπειρες λύσεις
, και άρα προκύπτουν οι άπειρες λύσεις  .
. , ο αριθμός είναι
, ο αριθμός είναι  .
. ή
ή  .
.
 .
.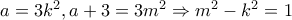 , αδύνατη.
, αδύνατη. , ο αριθμός είναι
, ο αριθμός είναι  .
. (το γινόμενο είναι γινόμενο 3 διαδοχικών φυσικών) και πρόκειται για τέλειο τετράγωνο, έχουμε
(το γινόμενο είναι γινόμενο 3 διαδοχικών φυσικών) και πρόκειται για τέλειο τετράγωνο, έχουμε  .
. , έστω
, έστω  , διαιρείται δια του
, διαιρείται δια του  , και οι άλλοι δύο,
, και οι άλλοι δύο,  , έχουν υπόλοιπα
, έχουν υπόλοιπα 
 .
. , άτοπο.
, άτοπο. , αδύνατη.
, αδύνατη. . Διακρίνω 3 περιπτώσεις:
. Διακρίνω 3 περιπτώσεις: πρώτος αριθμός.
πρώτος αριθμός. .
. σχηματίζουν πλήρες σύστημα υπολοίπων
σχηματίζουν πλήρες σύστημα υπολοίπων  .
. και οι υπόλοιποι έχουν γινόμενο
και οι υπόλοιποι έχουν γινόμενο  , από το θεώρημα Wilson.
, από το θεώρημα Wilson.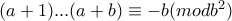 , άτοπο.
, άτοπο. τέλειο τετράγωνο. Τότε
τέλειο τετράγωνο. Τότε 
 .
.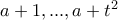 , υπάρχουν από περιστεροφωλιά τουλάχιστον 2 της μορφής
, υπάρχουν από περιστεροφωλιά τουλάχιστον 2 της μορφής  ,
,  .
.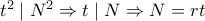

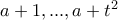 διαιρείται δια
διαιρείται δια  .
. διαιρεί το
διαιρεί το  .
. έχει πρώτο διαιρέτη
έχει πρώτο διαιρέτη  της μορφής
της μορφής  (ειδάλλως , δε θα ήταν της ίδιας μορφής).
(ειδάλλως , δε θα ήταν της ίδιας μορφής). , άτοπο.
, άτοπο. ούτε πρώτος ούτε τέλειο τετράγωνο.
ούτε πρώτος ούτε τέλειο τετράγωνο. στην αναπαράσταση του
στην αναπαράσταση του  , υψωμένος σε περιττή δύναμη, έστω
, υψωμένος σε περιττή δύναμη, έστω  .
. ,
, ,που διαιρούνται δια
,που διαιρούνται δια  .Δηλαδή,
.Δηλαδή,  .
. , και c περιττός, είναι
, και c περιττός, είναι 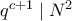 , άτοπο διότι ναι μεν
, άτοπο διότι ναι μεν  , αλλά
, αλλά 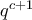 δε διαιρεί το
δε διαιρεί το  .
. , τότε
, τότε  , που διαιρούνται δια
, που διαιρούνται δια  .Δηλαδή,
.Δηλαδή, .
. , και c περιττός, είναι
, και c περιττός, είναι 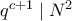 , άτοπο διότι ναι μεν
, άτοπο διότι ναι μεν  , αλλά
, αλλά 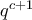 δε διαιρεί το
δε διαιρεί το  .
. .
. .
. τότε
τότε 
 τότε
τότε 
 δεν διαιρεί τόν
δεν διαιρεί τόν  και τα
και τα  αποτελούν πλήρες σύστημα υπολοίπων
αποτελούν πλήρες σύστημα υπολοίπων  .
.
 έχουμε
έχουμε  οπότε
οπότε 
 σύνθετος τότε:
σύνθετος τότε: τότε
τότε .
.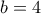 σαν τον
σαν τον  .
. τότε:
τότε: 
 και
και 
 αδύνατο.
αδύνατο.Με αφορμή το παραπάνω, παραπλήσιο στη μορφή πρόβλημα, γενικά:
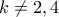 πολυώνυμο της μορφης
πολυώνυμο της μορφης  , οπου
, οπου  ρητός αριθμός, δεν ειναι τετράγωνο πολυωνύμου.
ρητός αριθμός, δεν ειναι τετράγωνο πολυωνύμου.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες