 καθώς και τον πρωτο
καθώς και τον πρωτο  ωστε ο αριθμος
ωστε ο αριθμος  να ειναι τέλειο τετραγωνο ακεραίου
να ειναι τέλειο τετραγωνο ακεραίουΣυντονιστές: cretanman, silouan, rek2
 καθώς και τον πρωτο
καθώς και τον πρωτο  ωστε ο αριθμος
ωστε ο αριθμος  να ειναι τέλειο τετραγωνο ακεραίου
να ειναι τέλειο τετραγωνο ακεραίου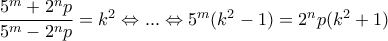
 πρέπει να είναι άρτιος, άρα ο
πρέπει να είναι άρτιος, άρα ο  πρέπει να είναι περιττός, έστω
πρέπει να είναι περιττός, έστω  , με
, με  μη αρνητικό ακέραιο.
μη αρνητικό ακέραιο.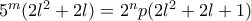
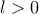 .
. , έχουμε ότι
, έχουμε ότι  , όπου
, όπου  θετικός ακέραιος.
θετικός ακέραιος. . Αν ο
. Αν ο  είναι άρτιος τότε πρέπει
είναι άρτιος τότε πρέπει  , όπου
, όπου  θετικός ακέραιος. Αν ο
θετικός ακέραιος. Αν ο  είναι περιττός, τότε
είναι περιττός, τότε  , άρα
, άρα  (δεν ισχύει). Σε κάθε περίπτωση έχουμε πως
(δεν ισχύει). Σε κάθε περίπτωση έχουμε πως  .
. και από το θεώρημα
και από το θεώρημα  ή το θεώρημα
ή το θεώρημα  παίρνουμε εύκολα ότι
παίρνουμε εύκολα ότι  , άρα
, άρα  και
και 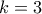 . Αντικαθιστώντας έχουμε πως
. Αντικαθιστώντας έχουμε πως  . Αν
. Αν  , τότε έχουμε το ζεύγος
, τότε έχουμε το ζεύγος  . Αν
. Αν  , έχουμε το ζεύγος
, έχουμε το ζεύγος  . Αν
. Αν  , τότε πρέπει
, τότε πρέπει  , άτοπο.
, άτοπο. . Τότε
. Τότε  , που είναι άτοπο, καθώς
, που είναι άτοπο, καθώς  1.
1. .
.Ευχαριστώ για την επισήμανση. Η λύση πάνω έχει κενό.JimNt. έγραψε:Είναι και η
 όπου
όπου  θετικός ακέραιος.
θετικός ακέραιος.


 και άρα
και άρα 
 Έστω ότι
Έστω ότι 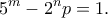 Τότε
Τότε 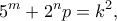 και άρα
και άρα  και
και 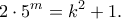 Από την τελευταία ισότητα έχουμε ότι ο
Από την τελευταία ισότητα έχουμε ότι ο  είναι περιττός, οπότε η σχέση
είναι περιττός, οπότε η σχέση

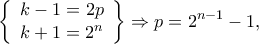

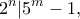 οπότε από το Λήμμα LTE (Lifting The Exponent) έχουμε ότι
οπότε από το Λήμμα LTE (Lifting The Exponent) έχουμε ότι
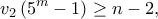 δηλαδή
δηλαδή  Αλλά τότε έχουμε ότι:
Αλλά τότε έχουμε ότι:
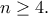 Οι περιπτώσεις
Οι περιπτώσεις  και
και  δεν μπορεί να ισχύουν, αλλά για
δεν μπορεί να ισχύουν, αλλά για  προκύπτει η λύση
προκύπτει η λύση 

 Όπως πριν, είναι
Όπως πριν, είναι  και άρα
και άρα
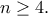 Εύκολα ελέγχουμε ότι οι περιπτώσεις
Εύκολα ελέγχουμε ότι οι περιπτώσεις 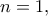
 και
και  δεν οδηγούν σε λύση.
δεν οδηγούν σε λύση. Έστω ότι
Έστω ότι  Τότε
Τότε  άτοπο.
άτοπο. Έστω ότι
Έστω ότι  Τότε, είναι υποχρεωτικά
Τότε, είναι υποχρεωτικά  οπότε
οπότε 

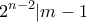 και άρα
και άρα
 Η περίπτωση
Η περίπτωση  δεν μπορεί να ισχύει, αλλά για
δεν μπορεί να ισχύει, αλλά για  προκύπτει η λύση
προκύπτει η λύση 
 Έστω ότι
Έστω ότι  Τότε
Τότε  άτοπο.
άτοπο. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες