 ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).
ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).Παραγοντοποίηση
Συντονιστές: cretanman, silouan, rek2
- Al.Koutsouridis
- Δημοσιεύσεις: 1798
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Παραγοντοποίηση
Να εκφράσετε τον αριθμό  ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).
ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).
 ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).
ως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).Λέξεις Κλειδιά:
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Παραγοντοποίηση
Θα χρησιμοποιήσουμε την ταυτότητα LagrangeAl.Koutsouridis έγραψε:Να εκφράσετε τον αριθμόως γινόμενο δυο παραγόντων (χωρίς χρήση υπολογιστή).
 .
.Θέτοντας
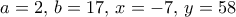 ,
,παίρνουμε
 από όπου το ζητούμενο.
από όπου το ζητούμενο. Κερδίζουμε ό,τι τολμούμε!
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15765
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Παραγοντοποίηση
Ας την συνεχίσουμε:Ορέστης Λιγνός έγραψε: παίρνουμεαπό όπου το ζητούμενο.
Δείξτε ότι η παραγοντοποίηση του Ορέστη είναι η μόνη δυνατή. Εννοείται ότι εξαιρούνται οι τετριμμένες μορφές όπως

Re: Παραγοντοποίηση
Μια ακόμη εφαρμογή : Βρείτε όλα τα ζεύγη διψήφιων φυσικών , των οποίων το γινόμενο να
γράφεται κατά δύο διαφορετικούς τρόπους , ως άθροισμα τετραγώνων δύο διψήφιων φυσικών .
γράφεται κατά δύο διαφορετικούς τρόπους , ως άθροισμα τετραγώνων δύο διψήφιων φυσικών .
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Παραγοντοποίηση
Θέλουμε να αποδείξουμε πως οιMihalis_Lambrou έγραψε:Ας την συνεχίσουμε:Ορέστης Λιγνός έγραψε: παίρνουμεαπό όπου το ζητούμενο.
Δείξτε ότι η παραγοντοποίηση του Ορέστη είναι η μόνη δυνατή. Εννοείται ότι εξαιρούνται οι τετριμμένες μορφές όπως
 και
και  είναι πρώτοι.
είναι πρώτοι.Αμφιβάλλω για το αν αυτή είναι η λύση που έχει στο νου του ο κύριος Μιχάλης και μπορεί να έχει κάποια λάθη. Βλέπουμε...
Καταρχάς θα αποδείξουμε πως αν
 ,τότε το
,τότε το  διαιρείται μόνο με πρώτους της μορφής
διαιρείται μόνο με πρώτους της μορφής  . Ισχύει το εξής λήμμα: Αν
. Ισχύει το εξής λήμμα: Αν  πρώτος της μορφής
πρώτος της μορφής  , τότε
, τότε  αν και μόνο αν
αν και μόνο αν  και
και  . Όμως
. Όμως  , άρα αν ο
, άρα αν ο  είναι σύνθετος, τότε θα διαιρείται μόνο από πρώτους της μορφής
είναι σύνθετος, τότε θα διαιρείται μόνο από πρώτους της μορφής  .
. Παρεμπιπτόντως οι αριθμοί
 και
και  δεν είναι αρκετά μεγάλοι και μπορούμε να δοκιμάσουμε αν διαιρούνται με κάποιον πρώτο της μορφής
δεν είναι αρκετά μεγάλοι και μπορούμε να δοκιμάσουμε αν διαιρούνται με κάποιον πρώτο της μορφής  μέχρι την τετραγωνική τους ρίζα.
μέχρι την τετραγωνική τους ρίζα.Κάνω όμως μια προσπάθεια χωρίς δοκιμές:
Ισχύει ακόμα πως κάθε πρώτος της μορφής
 είναι άθροισμα
είναι άθροισμα  τετραγώνων. Συνεπώς αν γράψουμε το
τετραγώνων. Συνεπώς αν γράψουμε το  στην κανονική του μορφή (αν είναι σύνθετος) τότε θα είναι κάπως έτσι:
στην κανονική του μορφή (αν είναι σύνθετος) τότε θα είναι κάπως έτσι: . Όμως ισχύει από την ταυτότητα
. Όμως ισχύει από την ταυτότητα  ότι
ότι 
Επαναλαμβάνοντας αυτή τη διαδικασία προκύπτει ότι
 . Πάλι από την ταυτότητα
. Πάλι από την ταυτότητα  προκύπτει ότι
προκύπτει ότι  και
και 
Εξετάζουμε με άλλα λόγια αν
 και αν
και αν  δηλαδή αν
δηλαδή αν  και αν
και αν  , όπου
, όπου 
Έχουμε

Ακόμη

 και επειδή
και επειδή  , προκύπτει ότι
, προκύπτει ότι  (αν
(αν  και
και  έτσι ώστε
έτσι ώστε  τότε η εξίσωση θα γινόταν
τότε η εξίσωση θα γινόταν  όπου προκύπτει ότι
όπου προκύπτει ότι  , δηλαδή
, δηλαδή  και
και  ).
). Άρα πρέπει να ισχύει ότι
 και ότι
και ότι  , δηλαδή
, δηλαδή  και ότι
και ότι  .
. Προσθέτουμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι
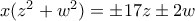 .
. Αναγκαστικά
 για τον ίδιο λόγο που
για τον ίδιο λόγο που  .
. Άρα έχουμε το σύστημα
 και
και  το οποίο δεν έχει ακέραιες λύσεις.
το οποίο δεν έχει ακέραιες λύσεις. Επομένως κάποιος από τους
 είναι ίσος με
είναι ίσος με  και έχουμε τετριμμένη παραγοντοποίηση, όπως
και έχουμε τετριμμένη παραγοντοποίηση, όπως  που απορρίπτεται. Συνεπώς
που απορρίπτεται. Συνεπώς  πρώτος και με παρόμοιο τρόπο αποδεικνύεται ότι o
πρώτος και με παρόμοιο τρόπο αποδεικνύεται ότι o  είναι πρώτος.
είναι πρώτος.Houston, we have a problem!
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15765
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Παραγοντοποίηση
Διονύσιος Αδαμόπουλος έγραψε: Θέλουμε να αποδείξουμε πως οικαι
είναι πρώτοι.
...
Παρεμπιπτόντως οι αριθμοίκαι
δεν είναι αρκετά μεγάλοι και μπορούμε να δοκιμάσουμε αν διαιρούνται με κάποιον πρώτο της μορφής
μέχρι την τετραγωνική τους ρίζα.
Ο απευθείας έλεγχος είναι βέβαια χειρονακτικός αλλά για τον
 που ελέγχουμε μόνο μέχρι τον
που ελέγχουμε μόνο μέχρι τον  , παλεύεται. Για τον
, παλεύεται. Για τον  πρέπει να πάμε μέχρι τον
πρέπει να πάμε μέχρι τον  , οπότε χρειάζεται να επιστρατεύσουμε Λογιστές. Με την ωραία όμως λύση του Διονύση που απευθύνεται σε Μαθηματικούς, τι να τους κάνουμε τους Λογιστές.
, οπότε χρειάζεται να επιστρατεύσουμε Λογιστές. Με την ωραία όμως λύση του Διονύση που απευθύνεται σε Μαθηματικούς, τι να τους κάνουμε τους Λογιστές.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
