 , θεωρούμε τυχόντα σημεία
, θεωρούμε τυχόντα σημεία  , ώστε τα τετράπλευρα
, ώστε τα τετράπλευρα να είναι κυρτά . Δείξτε ότι τα δύο αυτά τετράπλευρα , είναι επιπλέον και ισεμβαδικά .
να είναι κυρτά . Δείξτε ότι τα δύο αυτά τετράπλευρα , είναι επιπλέον και ισεμβαδικά .Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 , θεωρούμε τυχόντα σημεία
, θεωρούμε τυχόντα σημεία  , ώστε τα τετράπλευρα
, ώστε τα τετράπλευρα να είναι κυρτά . Δείξτε ότι τα δύο αυτά τετράπλευρα , είναι επιπλέον και ισεμβαδικά .
να είναι κυρτά . Δείξτε ότι τα δύο αυτά τετράπλευρα , είναι επιπλέον και ισεμβαδικά .Και τα 2 τετράπλευρα έχουν ίσες διαγώνιους που σχηματίζουν μεταξύ τους ίσες γωνίες
Εστω
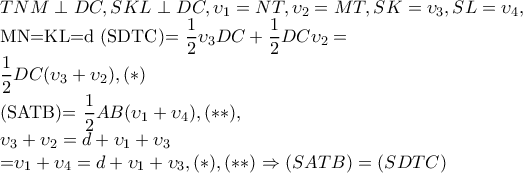
Είχα γράψει την λύση αλλά με πρόλαβε ο κ. Σταματογιάννης...έκανα ακριβώς το ίδιο.
 φέρνω παράλληλες στην
φέρνω παράλληλες στην  . Αυτές με τις παράλληλες ευθείες
. Αυτές με τις παράλληλες ευθείες 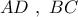 ορίζουν ένα νέο παραλληλόγραμμο
ορίζουν ένα νέο παραλληλόγραμμο  .
. , το ζητούμενο προφανές .
, το ζητούμενο προφανές . της περιμέτρου παραλληλογράμμου
της περιμέτρου παραλληλογράμμου  το τρίγωνο με κορυφή το
το τρίγωνο με κορυφή το  και βάση την απέναντι πλευρά
και βάση την απέναντι πλευρά Και μία τραβηγμένη (αφού τελείωσαν οι καλές ιδέες

 εδώ επεμβαίνει ο
εδώ επεμβαίνει ο 

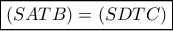
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες