Αναζητώντας τα μέγιστα

KARKAR · #1

: Αναζητώντας τα μέγιστα.png (9.53 KiB) Προβλήθηκε 884 φορές

Το τρίγωνο $\displaystyle ABC$ είναι ορθογώνιο - ισοσκελές . Σε σημείο

της

, με

, $( 0<x<\dfrac{a}{2})$ ,

υψώνουμε κάθετη , επί της οποίας - και στο εσωτερικό του τριγώνου - κινείται σημείο

του οποίου έστω

, η προβολή στην

. Οι

τέμνουν τα τμήματα SP,ST

στα σημεία D,E

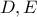αντίστοιχα .

α) Δείξτε ότι $DE\parallel BC$ . ...β) Αν η

τέμνει την

στο

, βρείτε την μέγιστη τιμή του (DQB)

και την περίμετρο του τριγώνου DQB

την στιγμή που το εμβαδόν του μεγιστοποιείται .

Xriiiiistos · #2

α) από θεώρημα θαλή έχουμε $\dfrac{PG}{GB}=\dfrac{ES}{TE}=\dfrac{EP}{CE}\Rightarrow GE//CB$

β) για τους υπολογισμούς AB=AC=a

και $\dfrac{BP}{BA}=s$ όπου s,a σταθερά (το P δεν κινείται)

Έστω $N\in AB$ ώστε TN//CB

τότε έχουμε

$\dfrac{TA}{DP}=\dfrac{TB}{BD}=\dfrac{NB}{GB}=\dfrac{DG}{TN}=s$ (I)

$(DGB)=\dfrac{DP\cdot GB}{2}\overset{(I)}{=}\dfrac{TA\cdot NB}{2s^{2}}\overset{(NB=TC)}{=}\dfrac{TA\cdot TC}{2s^{2}}=\dfrac{TA(a-TA)}{2s^{2}}$

Eπειδή τώρα το μόνο που μεταβάλεται είναι το TA το βλέπουμε σαν τριώνυμο με x=TA

( $f(x)=-x^{2}+ax$ ) που μεγιστοποιείται για $x=-\dfrac{a}{-1\cdot 2}=\dfrac{a}{2}$ (δεκτή). Άρα $SP=TA=\dfrac{a}{2}$ και γι'αυτήν την θέση έχουμε $(DGB)_{max}=\dfrac{TA(a-TA)}{2s^{2}}=\dfrac{a^{2}}{8\cdot s^{2}}$

Για την περίμετρο (P) έχουμε $P=DG+DB+GB\overset{(I)}{=}\dfrac{TN+TB+NB}{s}$
αφού T,N, τα μέσα των CA,AB $TN=\dfrac{CA}{2}=\dfrac{\sqrt{2}a}{2}\kappa \alpha \iota TB=\sqrt{a^{2}+(\dfrac{a}{2})^{2}}=\dfrac{\sqrt{5}}{2}a$ έχουμε

$P=\dfrac{\dfrac{1}{2}a+\dfrac{\sqrt{2}}{2}a+\dfrac{\sqrt{5}}{2}a}{s}=\dfrac{1+\sqrt{2}+\sqrt{5}}{2}\cdot \dfrac{a}{s}$

Μπορούσαμε επείσης να θέσουμε PB=t

( $\dfrac{t}{a}=s$ ) οπότε οι τύποι γίνονται

$(DGB)_{max}=\dfrac{a^{4}}{8\cdot t^{2}}\kappa \alpha \iota P=\dfrac{1+\sqrt{2}+\sqrt{5}}{2}\cdot \dfrac{a^{2}}{t}$

Αναζητώντας τα μέγιστα

Αναζητώντας τα μέγιστα

Re: Αναζητώντας τα μέγιστα

Μέλη σε σύνδεση