Γεωμετρικός τόπος από καθετότητα

#1

: Διαμετρική καθετότητα.png (12.66 KiB) Προβλήθηκε 725 φορές

Τα ημικύκλια διαμέτρων AB, AC (AB<AC)

εφάπτονται εσωτερικά στο

και έστω

ένα τυχαίο εσωτερικό σημείο του

τμήματος

. Από το

φέρνω κάθετο στην

που τέμνει το μικρό ημικύκλιο στο

και το μεγάλο στο

. Να βρείτε

τον γεωμετρικό τόπο του σημείου τομής

των

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

KARKAR · #2

: Παρατήρηση επί τόπου.png (16.3 KiB) Προβλήθηκε 720 φορές

Οι παρατηρήσεις όμως μπορούν να δημοσιευθούν άμεσα : Αν λοιπόν δείξουμε ,

ότι η

εφάπτεται του κύκλου που διέρχεται από τα M,B,C

, τότε

ο ζητούμενος γεωμετρικός τόπος είναι τμήμα κύκλου , κέντρου

και ακτίνας $AM=\sqrt{AB\cdot AC}$

S.E.Louridas · #3

Γεια και χαρά στους φίλους.
Τοποθετώ την ημέτερη άποψη στην Ανάλυση του θέματος κάνοντας άρση της απόκρυψης .

Ανάλυση: (Δείτε το αρχικό σχήμα του εισηγητή του θέματος):
Από το εγγεγραμμένο τετράπλευρο MFEA

παίρνουμε $\displaystyle{\angle EAF = \angle EMF.}$
Επίσης έχουμε $\displaystyle{\angle EFA = \angle FCB.}$
Άρα ισχύει $\displaystyle{\vartriangle MBC \sim \vartriangle AEF \Rightarrow \frac{{MC}}{{MB}} = \sqrt {\frac{{A{F^2}}}{{A{E^2}}}} \Rightarrow \frac{{MC}}{{MB}} = \sqrt {\frac{{AC}}{{AB}}} ,\;\;ct.}$
Έτσι πάμε σε τμήμα Απολλώνιου κύκλου...

#4

Καλό μεσημέρι σε όλους!

: Διαμετρική καθετότητα.II.png (27.24 KiB) Προβλήθηκε 618 φορές

Η εφαπτομένη του μπλε ημικυκλίου στο

τέμνει το κόκκινο ημικύκλιο στο

. Το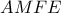

είναι εγγράψιμο (δύο από τις

απέναντι γωνίες του είναι ορθές). Άρα $A\widehat MF=A\widehat EN= E\widehat BN$ , δηλαδή τα τρίγωνα AMC, AMB

είναι όμοια.

$\displaystyle{\frac{{MA}}{{AB}} = \frac{{AC}}{{MA}} \Leftrightarrow M{A^2} = AB \cdot AC = A{T^2} \Leftrightarrow }$ $\boxed{AM=AT=ct}$ Το

κινείται λοιπόν σε κύκλο κέντρου

και

ακτίνας

. Επειδή όμως το

είναι σημείο του τμήματος

, ο ζητούμενος γεωμετρικός τόπος περιορίζεται στο τόξο $\overset\frown{TS}.$

Γεωμετρικός τόπος από καθετότητα

Γεωμετρικός τόπος από καθετότητα

Re: Γεωμετρικός τόπος από καθετότητα

Re: Γεωμετρικός τόπος από καθετότητα

Re: Γεωμετρικός τόπος από καθετότητα

Μέλη σε σύνδεση