 ορίζουμε ως
ορίζουμε ως  τον μικρότερο από από τους
τον μικρότερο από από τους  . Να βρεθεί η μέγιστη δυνατή τιμή του
. Να βρεθεί η μέγιστη δυνατή τιμή του  .
.Σχόλιο. Η άσκηση είναι επουσιώδης παραλλαγή (άλλα νούμερα) αλλά, κυρίως, βελτίωση μιας άσκησης που μου έστειλαν χθες από Ρουμανία. Ήταν από διαγωνισμό σε Β' Γυμνασίου. Μου άρεσε πολύ γι' αυτό την μοιράζομαι μαζύ σας.

 . Ας υποθέσουμε ότι
. Ας υποθέσουμε ότι  .
.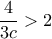 , άρα
, άρα  . Οπότε,
. Οπότε,  συνεπώς
συνεπώς  . Άρα,
. Άρα,
 , τότε ισχύει ότι
, τότε ισχύει ότι  .
. .
.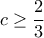 τότε
τότε  , και είμαστε εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι
, και είμαστε εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι  .
.  τότε
τότε  , και είμαστε πάλι εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι
, και είμαστε πάλι εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι  .
. τότε
τότε  , και είμαστε πάλι εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι
, και είμαστε πάλι εντάξει. Μπορούμε λοιπόν να υποθέσουμε ότι  .
. , που ολοκληρώνει την απόδειξη του
, που ολοκληρώνει την απόδειξη του  είναι
είναι  που ολοκληρώνει την άσκηση.
που ολοκληρώνει την άσκηση.

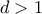




 είναι ίσο με π.χ. την πρώτη συντεταγμένη (όμοια οι άλλες περιπτώσεις), τότε μεγαλώνοντας ελάχιστα το
είναι ίσο με π.χ. την πρώτη συντεταγμένη (όμοια οι άλλες περιπτώσεις), τότε μεγαλώνοντας ελάχιστα το  (αλλά να παραμένει μικρότερο από τις άλλες συντεταγμένες) έχει ως αποτέλεσμα να μεγαλώνει το minimum. Άρα περιμένουμε ότι το μέγιστο minimum να έχει όλες τις συντεταγμένες ίσες, εδώ
(αλλά να παραμένει μικρότερο από τις άλλες συντεταγμένες) έχει ως αποτέλεσμα να μεγαλώνει το minimum. Άρα περιμένουμε ότι το μέγιστο minimum να έχει όλες τις συντεταγμένες ίσες, εδώ  . Λύνοντας το σύστημα θα βρούμε τις τιμές που έγραψα στην λύση μου (όπως και ο Ορέστης), δηλαδή
. Λύνοντας το σύστημα θα βρούμε τις τιμές που έγραψα στην λύση μου (όπως και ο Ορέστης), δηλαδή