Να δείξετε ότι
 ,
,για όλους τους θετικούς πραγματικούς αριθμούς
 .
.Συντονιστές: achilleas, emouroukos, silouan
 ,
, .
.Είναι πολύ γνωστή.


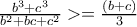
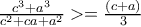
 θετικοί πραγματικοί αριθμοί, τότε
θετικοί πραγματικοί αριθμοί, τότε 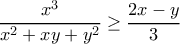 .
.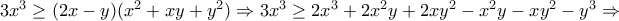

 , που ισχύει.
, που ισχύει. .
.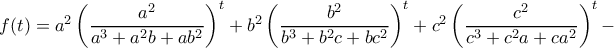
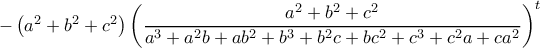
 , δηλαδή δυο λύσεις. Άρα, σύμφωνα με το παραπάνω θεώρημα, δεν θα υπάρχουν άλλες λύσεις.
, δηλαδή δυο λύσεις. Άρα, σύμφωνα με το παραπάνω θεώρημα, δεν θα υπάρχουν άλλες λύσεις.
 .
. θα είναι μεγαλύτερος από τον
θα είναι μεγαλύτερος από τον  και κάποιος μικρότερος.
και κάποιος μικρότερος. τείνοντος στο συν άπειρο, παρατηρούμε ότι ο επικρατέστερος όρος, ο μεγαλύτερος (ή μικρότερος), αυτός που θα καθορίσει το πρόσημο, είναι μεταξύ των
τείνοντος στο συν άπειρο, παρατηρούμε ότι ο επικρατέστερος όρος, ο μεγαλύτερος (ή μικρότερος), αυτός που θα καθορίσει το πρόσημο, είναι μεταξύ των  .
. 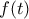 είναι θετική για μεγάλα
είναι θετική για μεγάλα  . Επειδή πέραν των ριζών
. Επειδή πέραν των ριζών  άλλες δεν υπάρχουν, η
άλλες δεν υπάρχουν, η 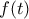 διατηρεί πρόσημο για
διατηρεί πρόσημο για 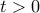 και θα είναι
και θα είναι  .
.


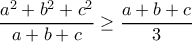
 έχουμε ισότητα.
έχουμε ισότητα.Επιπλέον τέθηκε ως πρόβλημα 1 στο πρώτο τέστ επιλογής βουλγαρικής ομάδας για τηνAl.Koutsouridis έγραψε: ↑Παρ Απρ 30, 2021 7:35 pmΗ ανισότητα αυτή είχε τεθεί στον Ευκλείδη του 2000-2001 για την Γ' Λυκείου viewtopic.php?f=58&t=32938
Εμφανίζεται και στο περιοδικό Κβαντ (M969, 1986, 2o τεύχος)
 περιση.
περιση.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες