 ώστε:
ώστε:i) οι
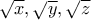 είναι πλευρές τριγώνου, και
είναι πλευρές τριγώνου, και ii)
 .
.Να αποδείξετε, ότι:
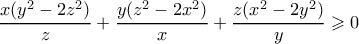 .
.Συντονιστές: achilleas, emouroukos, silouan
 ώστε:
ώστε: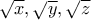 είναι πλευρές τριγώνου, και
είναι πλευρές τριγώνου, και  .
.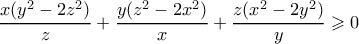 .
.Δηλαδή ,κάνοντας τις διαιρέσεις,αρκεί να αποδείξουμε ότιΟρέστης Λιγνός έγραψε: ↑Δευ Αύγ 10, 2020 11:55 pmΈστωώστε:
i) οιείναι πλευρές τριγώνου, και
ii).
Να αποδείξετε, ότι:
.
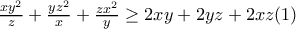
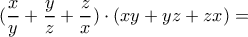
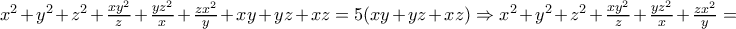
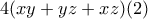
 πρέπει να ισχύει
πρέπει να ισχύει 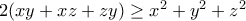 από το
από το 
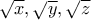 είναι πλευρές τριγώνου.Σχετικό θέμα εδώ https://artofproblemsolving.com/communi ... equalities
είναι πλευρές τριγώνου.Σχετικό θέμα εδώ https://artofproblemsolving.com/communi ... equalitiesΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 19 επισκέπτες