 είναι θετικοί αν αποδείξετε
είναι θετικοί αν αποδείξετε 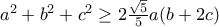
Πηγή Αops
Συντονιστές: achilleas, emouroukos, silouan
Είναι
![4b^{2}-4c+c^{2}\geq 4b^{2}-4bc+c^{2}=\left ( 2b-c \right )^{2}\geq 0\Leftrightarrow 4b^{2}-4c+c^{2}=5b^{2}+5c^{2}-b^{2}-4c-4c^{2}=b^{2}+c^{2}-\frac{b^{2}+4c+4c^{2}}{5}\Leftrightarrow a^{2}+b^{2}+c^{2}+\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\frac{b^{2}+4c+4c^{2}}{5}-a^{2}=a^{2}+b^{2}+c^{2}+..\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\left [ \frac{\sqrt{5}\left ( b+2c \right )}{5} \right ]^{2}-a^{2}\geq 0 4b^{2}-4c+c^{2}\geq 4b^{2}-4bc+c^{2}=\left ( 2b-c \right )^{2}\geq 0\Leftrightarrow 4b^{2}-4c+c^{2}=5b^{2}+5c^{2}-b^{2}-4c-4c^{2}=b^{2}+c^{2}-\frac{b^{2}+4c+4c^{2}}{5}\Leftrightarrow a^{2}+b^{2}+c^{2}+\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\frac{b^{2}+4c+4c^{2}}{5}-a^{2}=a^{2}+b^{2}+c^{2}+..\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\left [ \frac{\sqrt{5}\left ( b+2c \right )}{5} \right ]^{2}-a^{2}\geq 0](/forum/ext/geomar/texintegr/latexrender/pictures/e8917cf603e4fd9d22114f4471da5ef5.png)
 αντικαθιστώντας έχουμε :
αντικαθιστώντας έχουμε :![a^{2}+b^{2}+c^{2}+\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\left [ \frac{\sqrt{5}\left ( b+2c \right )}{5} \right ]^{2}-a^{2}\geq 0 \Leftrightarrow a^{2}+b^{2}+c^{2}+(x-a)^{2}-x^{2}-a^{2}=a^{2}+b^{2}+c^{2}+x^{2}-2ax+a^{2}-x^{2}-a^{2}=a^{2}+b^{2}+c^{2}-2ax\geq 0\Leftrightarrow a^{2}+b^{2}+c^{2}-2a\frac{\sqrt{5}(b+2c)}{5}\geq 0\Leftrightarrow a^{2}+b^{2}+c^{2}\geq 2a\frac{\sqrt{5}(b+2c)}{5} a^{2}+b^{2}+c^{2}+\left [ \frac{\sqrt{5}}{5}(b+2c)-a \right ]^{2}-\left [ \frac{\sqrt{5}\left ( b+2c \right )}{5} \right ]^{2}-a^{2}\geq 0 \Leftrightarrow a^{2}+b^{2}+c^{2}+(x-a)^{2}-x^{2}-a^{2}=a^{2}+b^{2}+c^{2}+x^{2}-2ax+a^{2}-x^{2}-a^{2}=a^{2}+b^{2}+c^{2}-2ax\geq 0\Leftrightarrow a^{2}+b^{2}+c^{2}-2a\frac{\sqrt{5}(b+2c)}{5}\geq 0\Leftrightarrow a^{2}+b^{2}+c^{2}\geq 2a\frac{\sqrt{5}(b+2c)}{5}](/forum/ext/geomar/texintegr/latexrender/pictures/fd49f113c4e00d49a021c704ee35c888.png)
Η ανισότητα ισοδύναμα γράφεται

 . Αρκεί να δείξουμε ότι η διακρίνουσά του
. Αρκεί να δείξουμε ότι η διακρίνουσά του  είναι μη θετική. Πράγματι
είναι μη θετική. Πράγματι![\displaystyle D = \left [ 2\frac{\sqrt{5}}{5}a(b+2c) \right ]^2-4 \left ( b^2+c^2 \right ) = \displaystyle D = \left [ 2\frac{\sqrt{5}}{5}a(b+2c) \right ]^2-4 \left ( b^2+c^2 \right ) =](/forum/ext/geomar/texintegr/latexrender/pictures/672a449ce83b02218251a9ba94f2bc82.png)




 ή
ή  .
.Έχεις δίκιο, είχα στο μυαλό μου ότιXriiiiistos έγραψε: ↑Δευ Νοέμ 26, 2018 2:51 pmΑυτό είναι λάθος γιατί αντο αριστερό μέλος θα είναι μικρότερο από το δεξί
 .
. μάλλον εννοούσες
μάλλον εννοούσες  αφού ο b είναι θετικός)
αφού ο b είναι θετικός)Παρατηρούμε ότι η δεδομένη ανισοτική έκφραση είναι ομογενές πολυώνυμο δευτέρου βαθμού (κάθε μονώνυμο που την αποτελεί είναι δευτέρου βαθμού).
 (κάποιο μονώνυμο δευτέρου βαθμού) με την ελπίδα ότι θα προκύψη πιο απλή έκφραση με λιγότερες μεταβλητές. Έχουμε ισοδύναμα
(κάποιο μονώνυμο δευτέρου βαθμού) με την ελπίδα ότι θα προκύψη πιο απλή έκφραση με λιγότερες μεταβλητές. Έχουμε ισοδύναμα
 ,
, 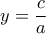 η ανισότητα γίνεται
η ανισότητα γίνεται



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης